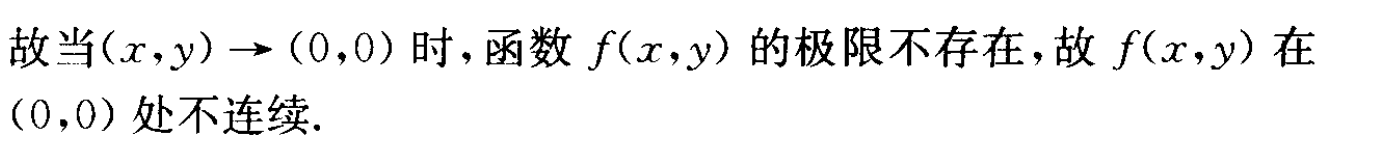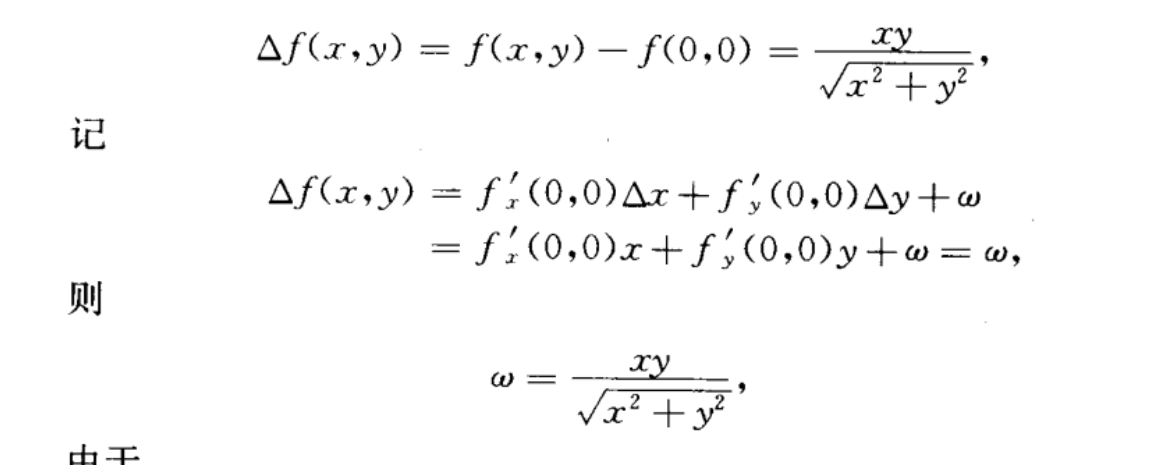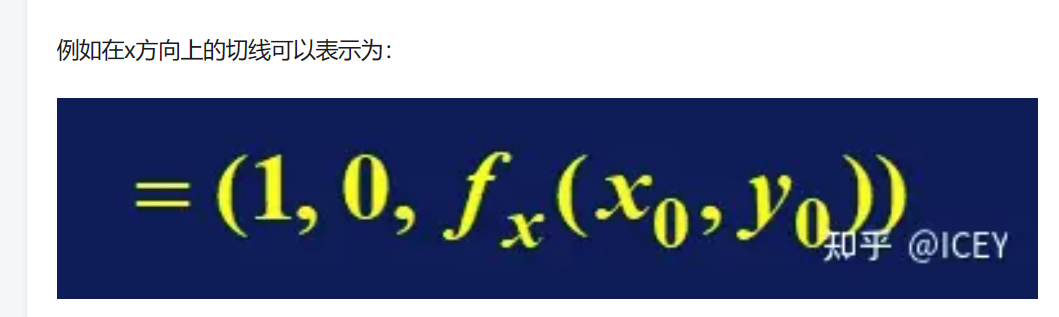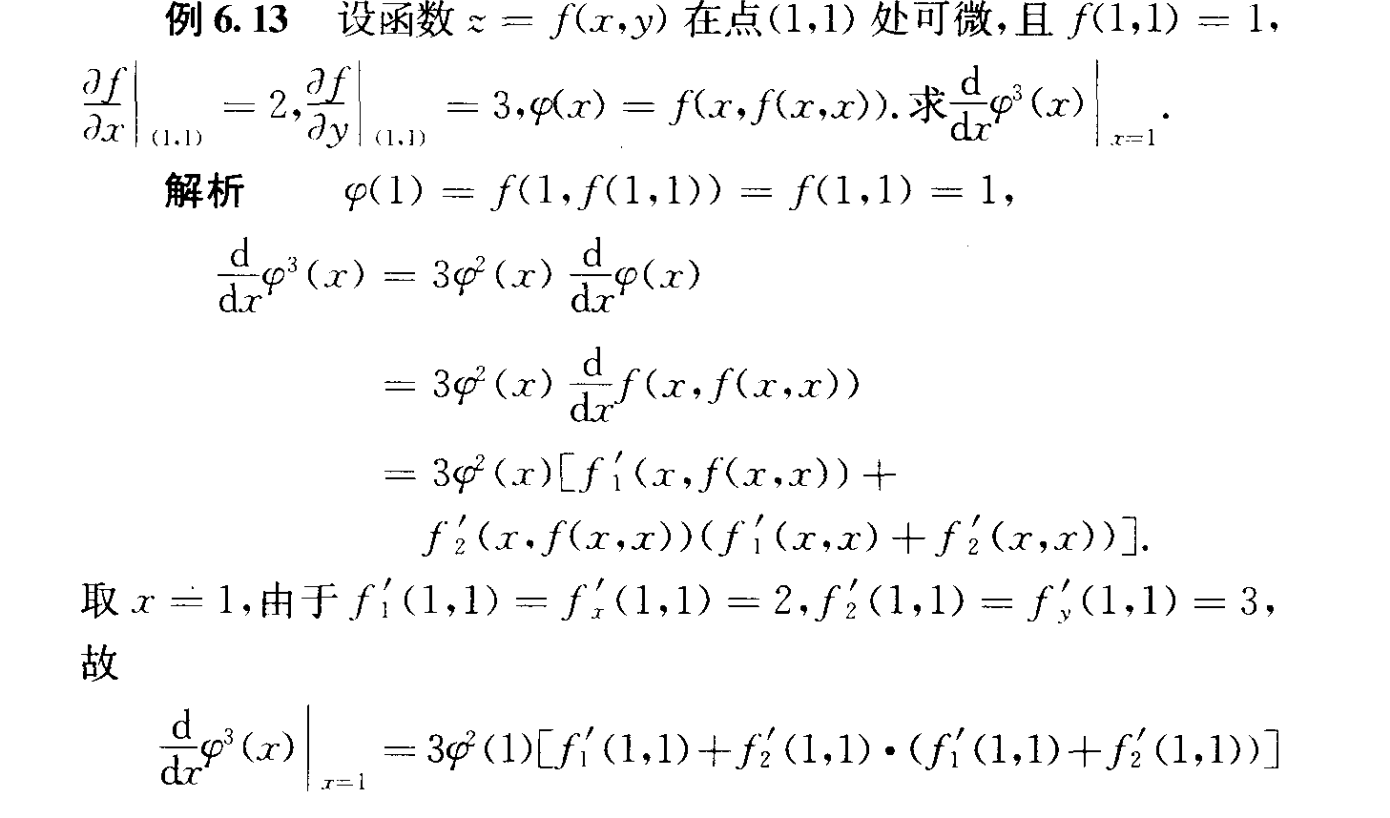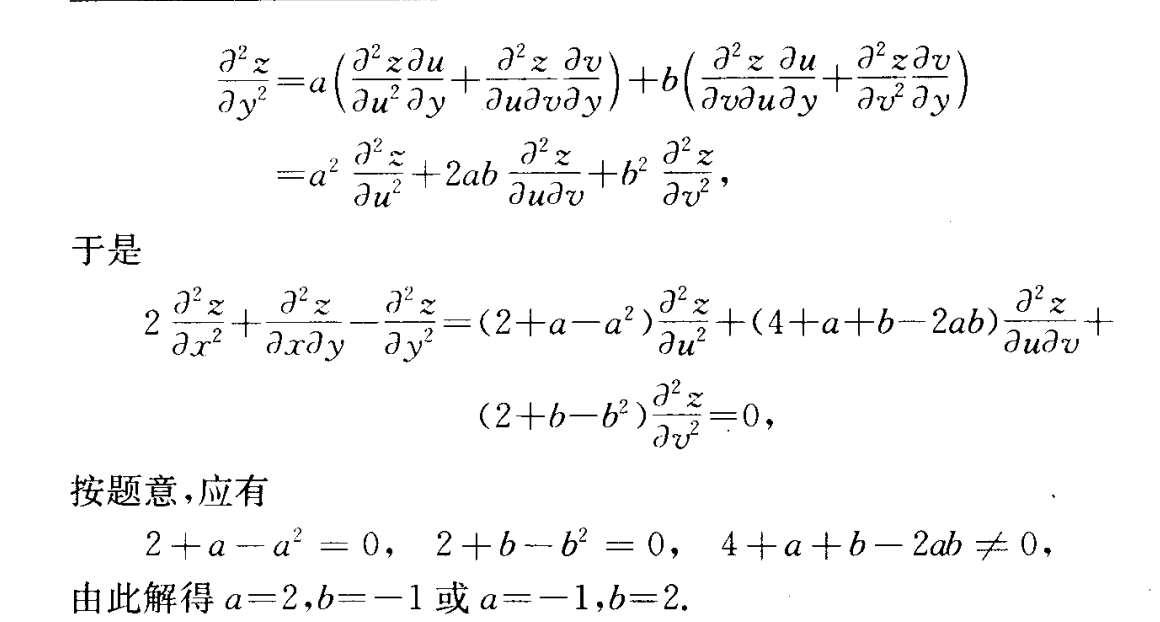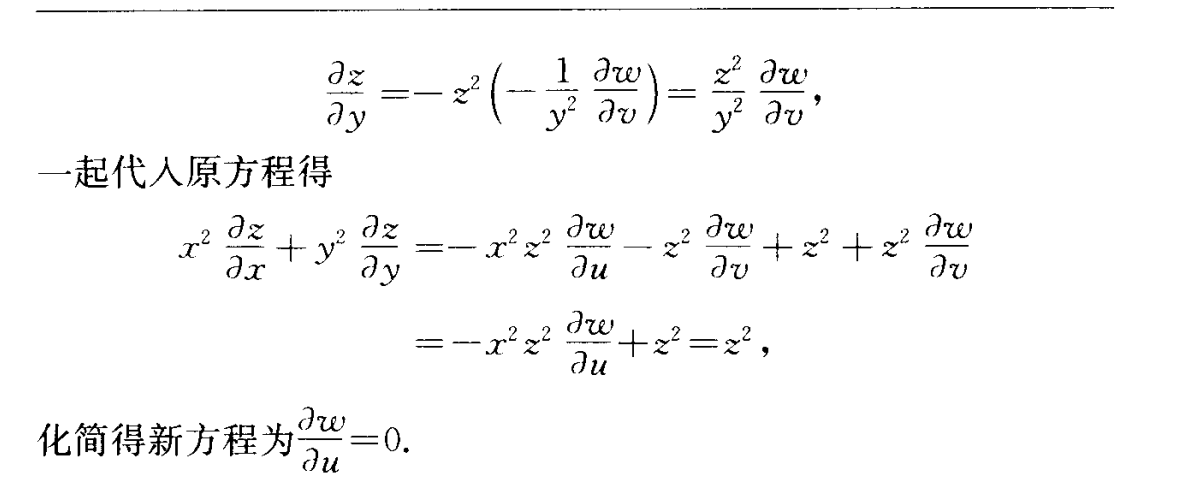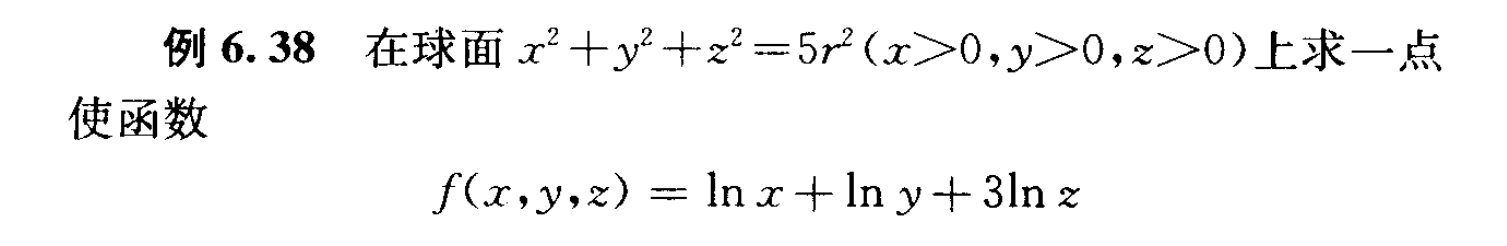6 多元函数微分学

6.1使用不等式放缩求极限

image-20240311185455296

6.3 沿直线时记得讨论x=0的直线

image-20240311190258396

image-20240311190315679

6.4&6.5 分段函数连续、可偏导、可微、连续可微的讨论

  • 连续直接判断分段函数另一段趋近于某一点时极限是不是某一点处的值

  • 偏导用定义来证（让其中一个变量趋近于0，另一个变量等于0）

  • 可微用
    $
    \Delta{z}=f(x,y)-f(0,0)=f^{'}{x}(0,0)\Delta{x}+f^{'}{y}(0,0)\Delta{y}+w
    $
    求出w后除以$\sqrt{x^2+y^2}$

    PS:求w时如果$\Delta{x}和\Delta{y}$消不掉的话，就直接把他们换成x和y

    image-20240311191644850

  • 连续可微即两个偏导数还连续（证明方法是先求导，然后用定义求出分段点的偏导数值，看与求导的极限是否相等），是最强的条件，连续可微一定可微

  • 实例：

image-20240311191216036

6.6 偏导数的几何意义

image-20240311194237109

image-20240311194247434

image-20240311194316473

6.13 多重求导

image-20240311201318411

6.14 求dz说明z和x、y有关系

image-20240311201659671

6.17 6.18 利用隐函数求导计算参数间的关系

image-20240311202641829

image-20240311202957347

6.19 切平面法向量的确定方式

image-20240311203132017

image-20240311203356939

6.20 隐函数求导后积分求原函数

image-20240311203634963

6.27 注意求二阶偏导时z就和xy有关了

image-20240311204902959

6.28 二阶求偏导注意变量和其他哪些变量有关系

image-20240408091841299

image-20240408091855468

6.29 通过偏导变化来改变方程形式

image-20240408092604560

image-20240408092616222

6.30 齐次式证明

image-20240408094254971

image-20240408094302537

6.31 求极值时对$B^2-AC=0$进行单独讨论

image-20240408160355153

image-20240408160404338

6.34 利用拉格朗日乘数法求距离最小值

image-20240408162349264

image-20240408162400305

6.35 拉格朗日乘数法后证明不等式

image-20240408163928648

image-20240408163942338