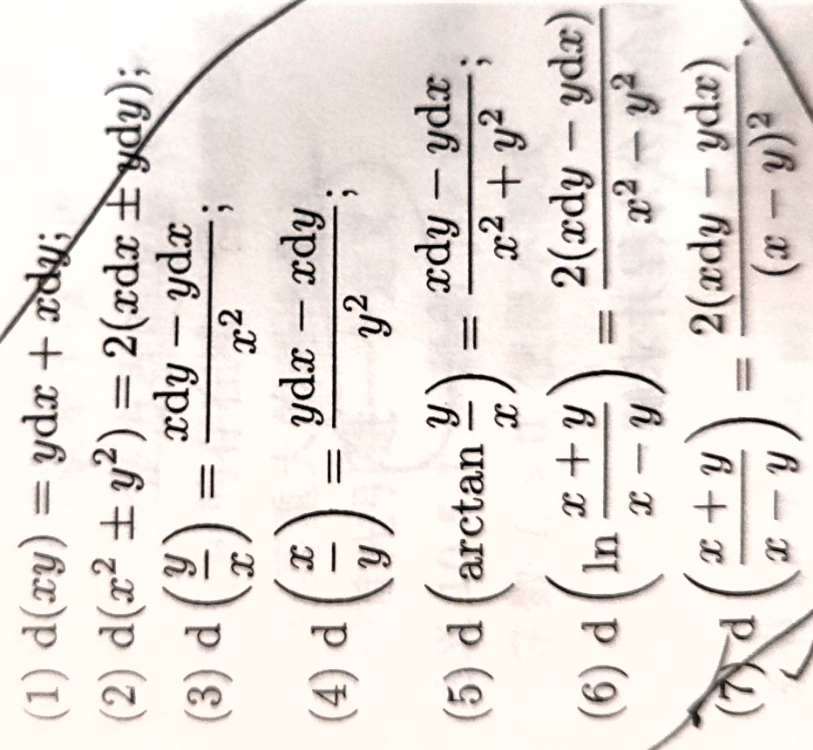
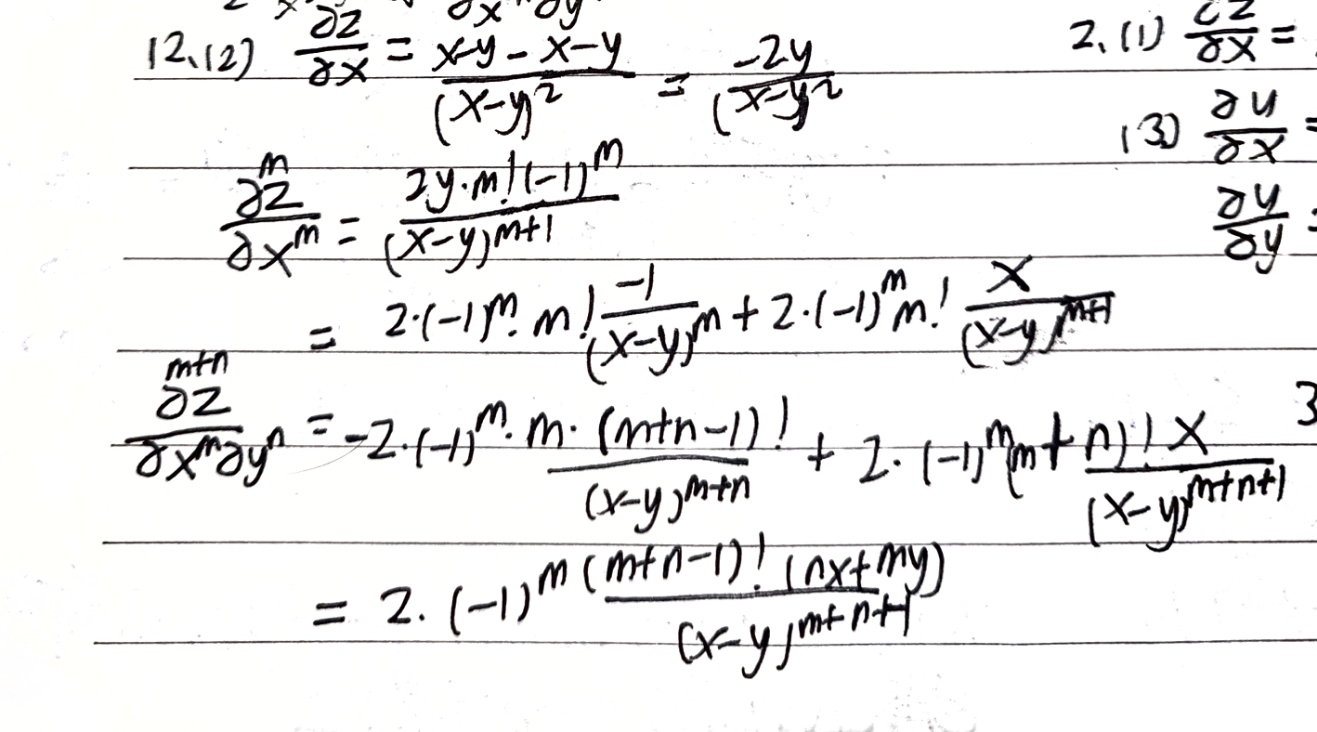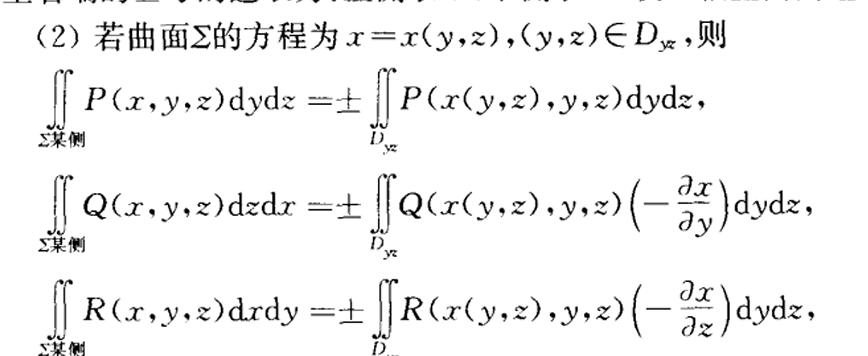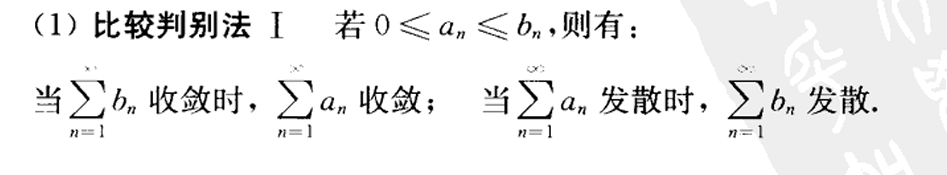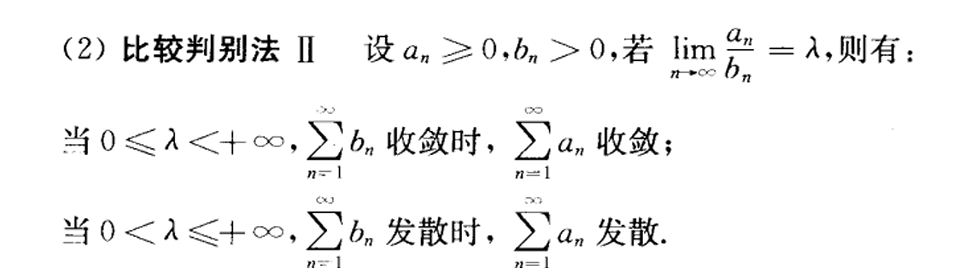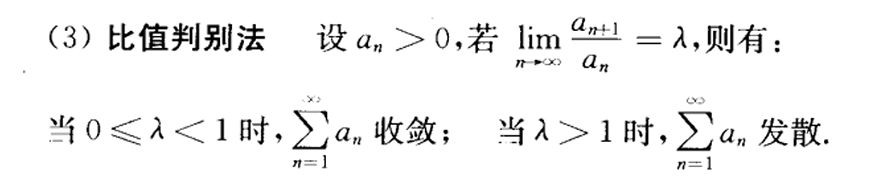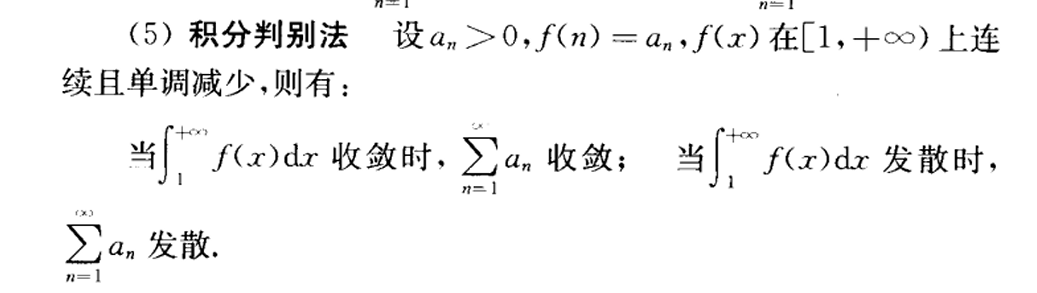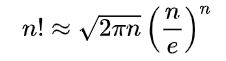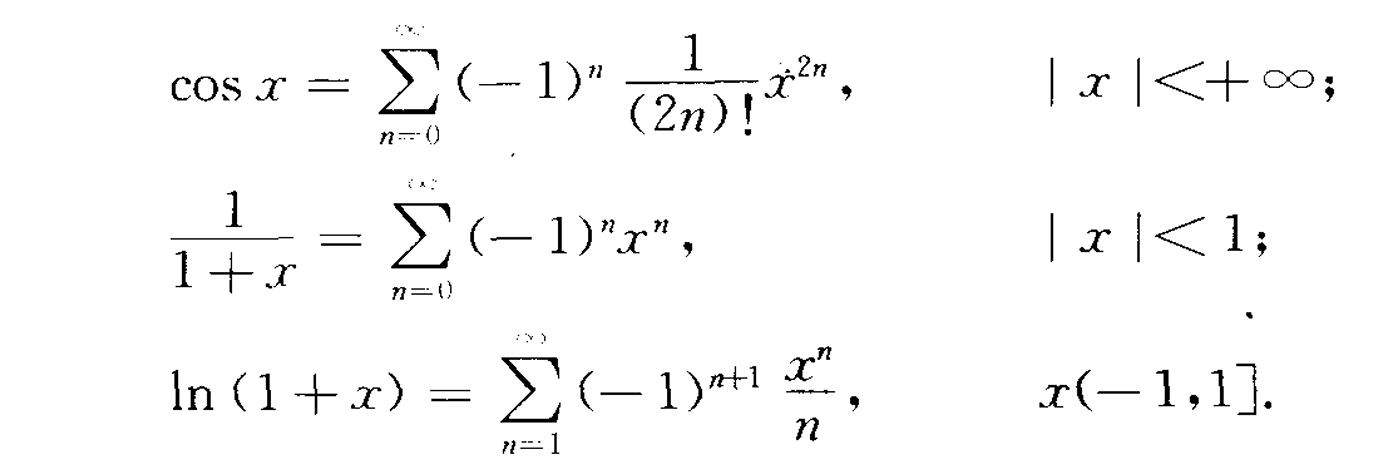多元函数微分学
多元函数的极限与连续性
定义
-
邻域$N_{\delta}(P0)$
-
内点、外点、边界、聚点(内点一定是聚点,边界点可能是聚点)
-
开集、闭集、连通集、开区域、闭区域、有界集、无界集
-
多元函数
-
二元函数的二重极限
二重极限存在当且仅当以任何方式趋向点p时,都趋向同一个常数A,否则极限不存在。
证无极限:1. 找极限不存在的路径(无穷)2. 找极限不相等的路径
求极限方法:1. 利用定义放缩证明\夹逼准则放缩 2.换元法,常用三角换元
-
累次极限则趋向时有先后顺序
-
多元函数的连续性:
连续性产生的4大性质:
偏导数与全微分
-
偏导数
-
高阶偏导数
不连续函数求某个点偏导数值方法:(使用定义)
高阶偏导例题:
-
全微分
证明不可微的方法:求w,看是不是P的高阶无穷小$\Delta{z}=f(x,y)-f(0,0)=f’x(0,0)x+f’y(0,0)y+w$
-
连续可微:导函数连续=>推出可微
-
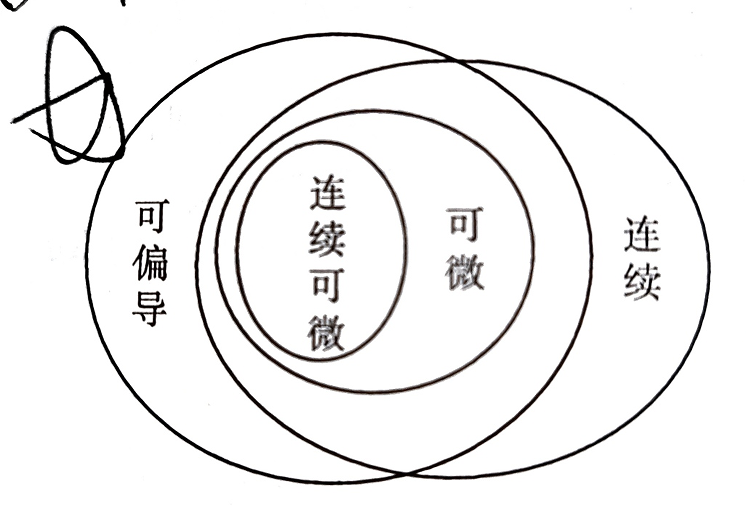
关系
复合函数与隐函数的偏导数
-
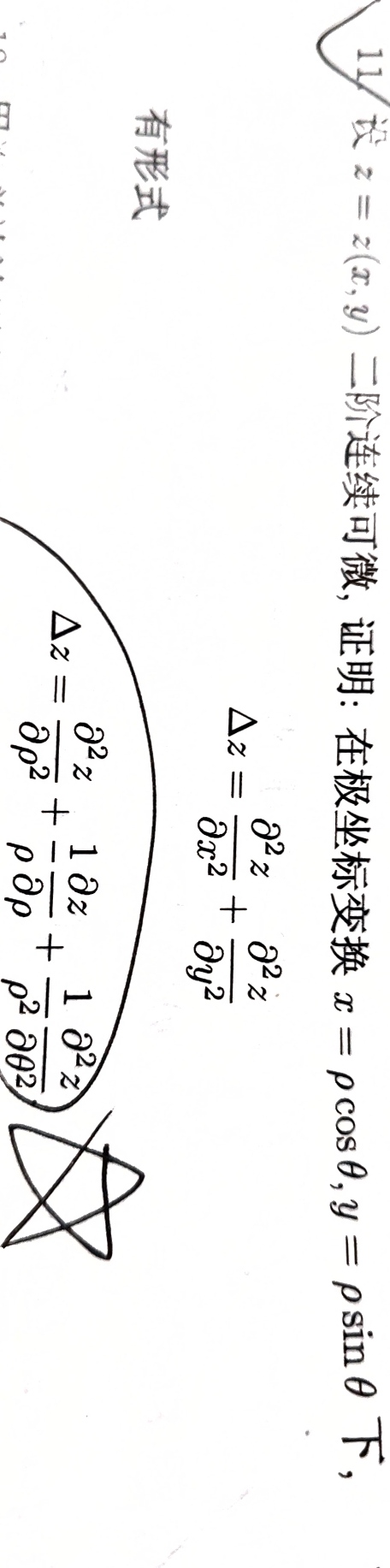
复合函数的偏导数:三个链式法则
-
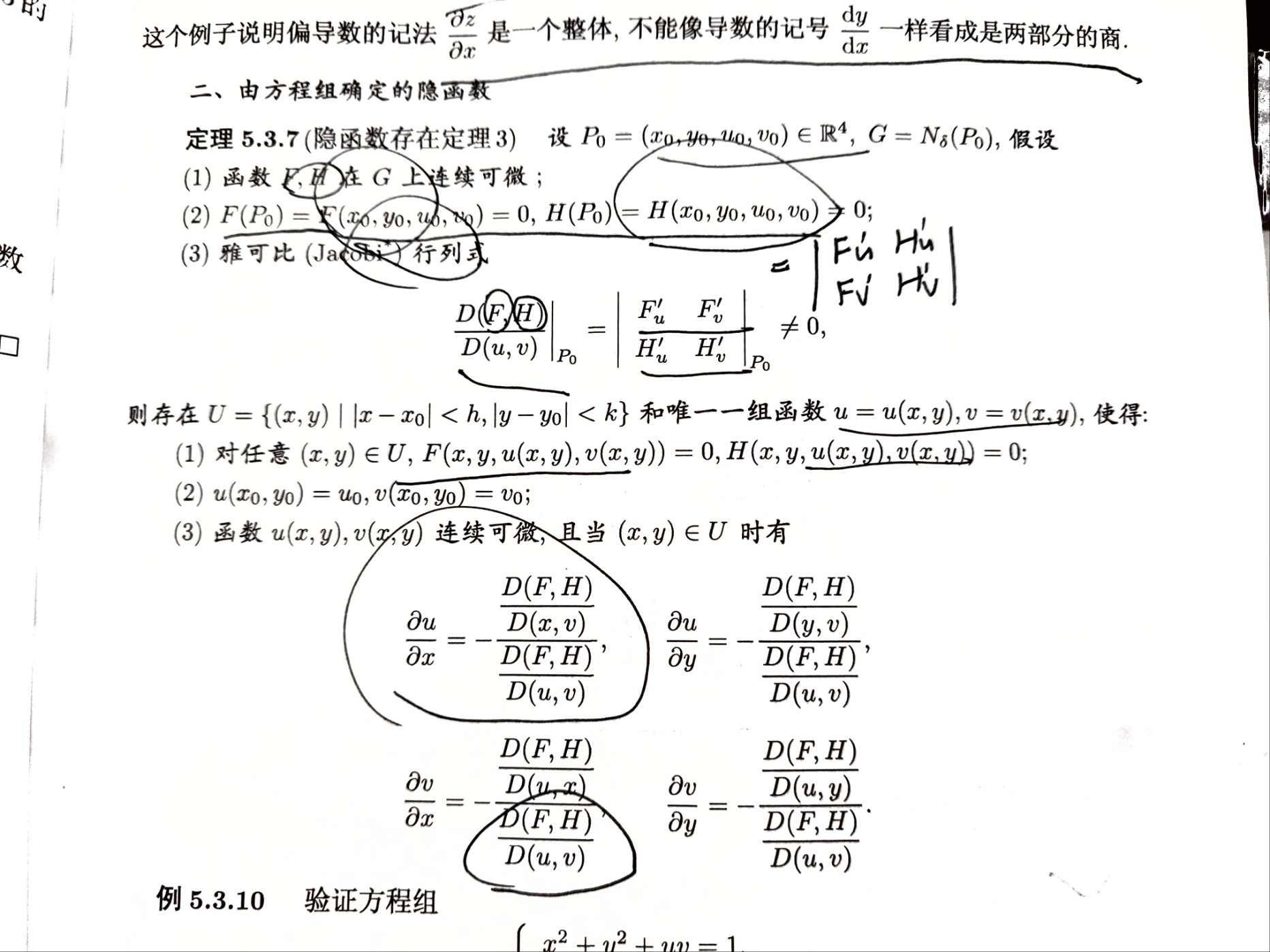
隐函数的偏导数
注意求一阶偏导时各变量无关系,求谁把其他当做常量,但求二阶时变量之间有关系。
若方程为z,x,y的关系,现在要求z与x的偏导关系和y与x的偏导关系,则可以用$\frac{\partial{y}}{\part{x}}=-\frac{\frac{D(F,H)}{D(x,z)}}{\frac{D(F,H)}{D(y,z)}}$
多元向量函数
结论:习题1和2中的两个式子若对于一个r是相等的。
偏导数在几何上的应用
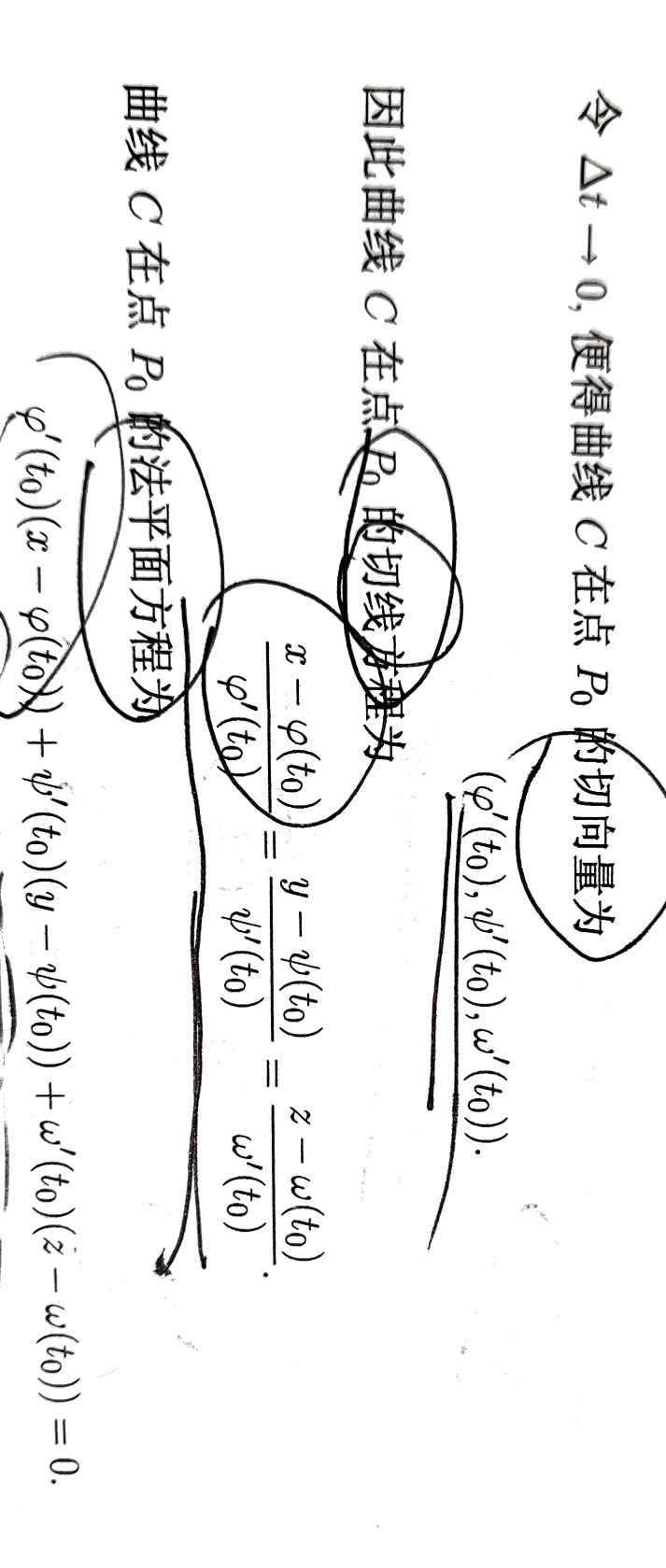
空间曲线的切线与法平面
-
对于参数方程
-
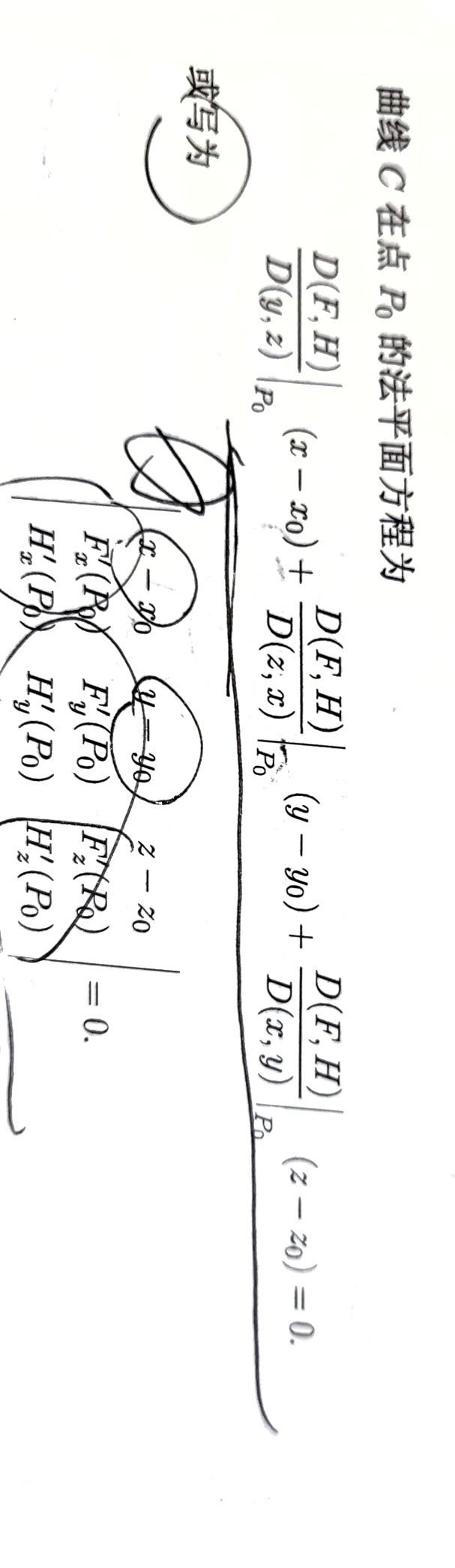
对于一般方程
空间曲面的切平面与发现
-
一般式方程
-
参数方程
好题:
极值与条件极值
-
可疑极值点:包括驻点和不可偏导的点
-
极值判别法中:$B^2-AC=0$单独讨论,可用定义证明即找一个邻域看是不是都大于极值点值或小于极值点值;也可用极值判别法1证$u=f’x(x-x0)+f’y(y-y0)$
-
最值
-
条件极值
方向导数
重积分
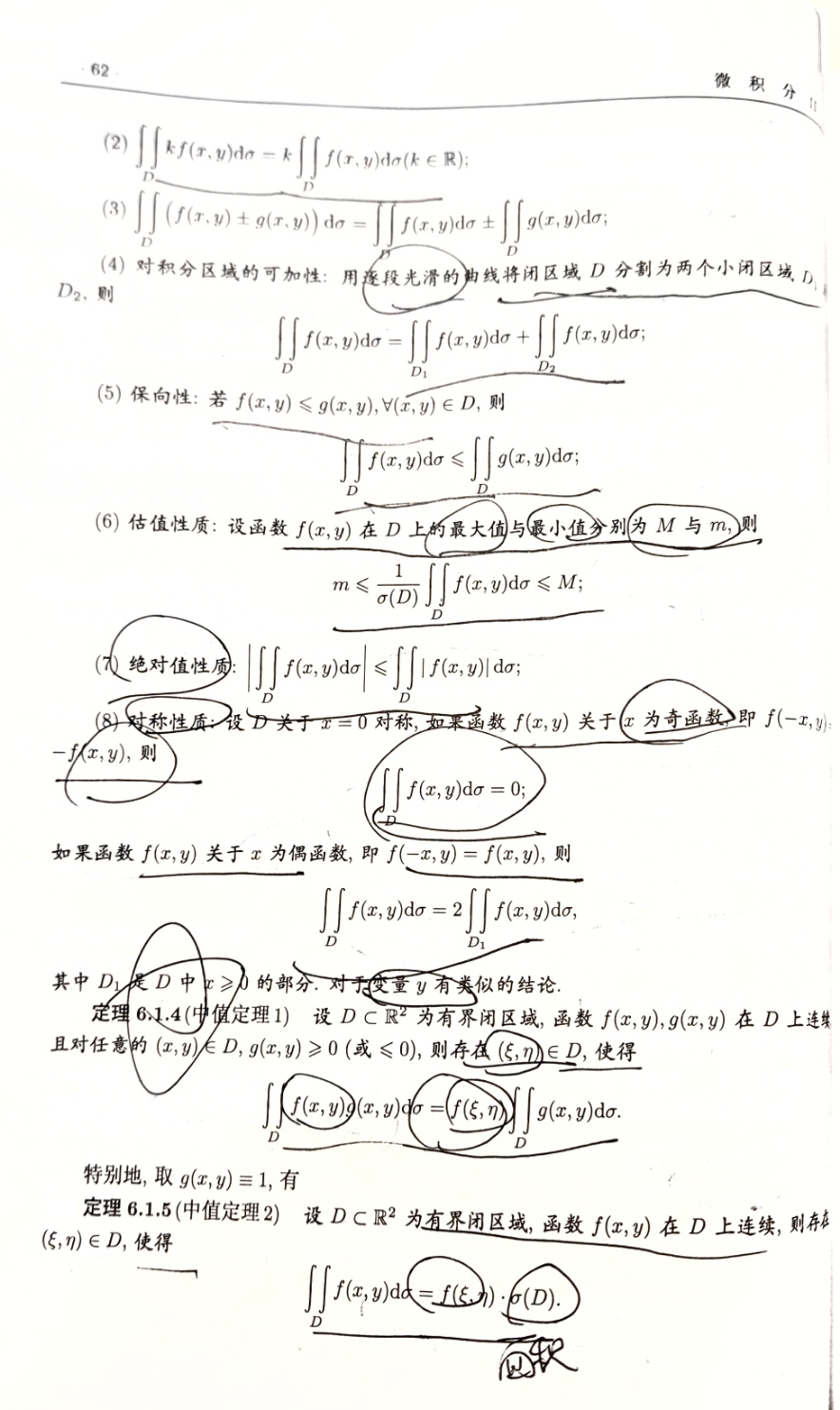
二重积分的概念和性质
二重积分的相关性质:
二重积分的计算
三重积分
累次积分法:
换元积分法:
曲线积分
第一二类曲线积分
注意a一定满足小于b,即第一类曲线积分不关注起点终点,一定从小积到大
第二类曲线积分有方向要求,必须从起点积到终点。
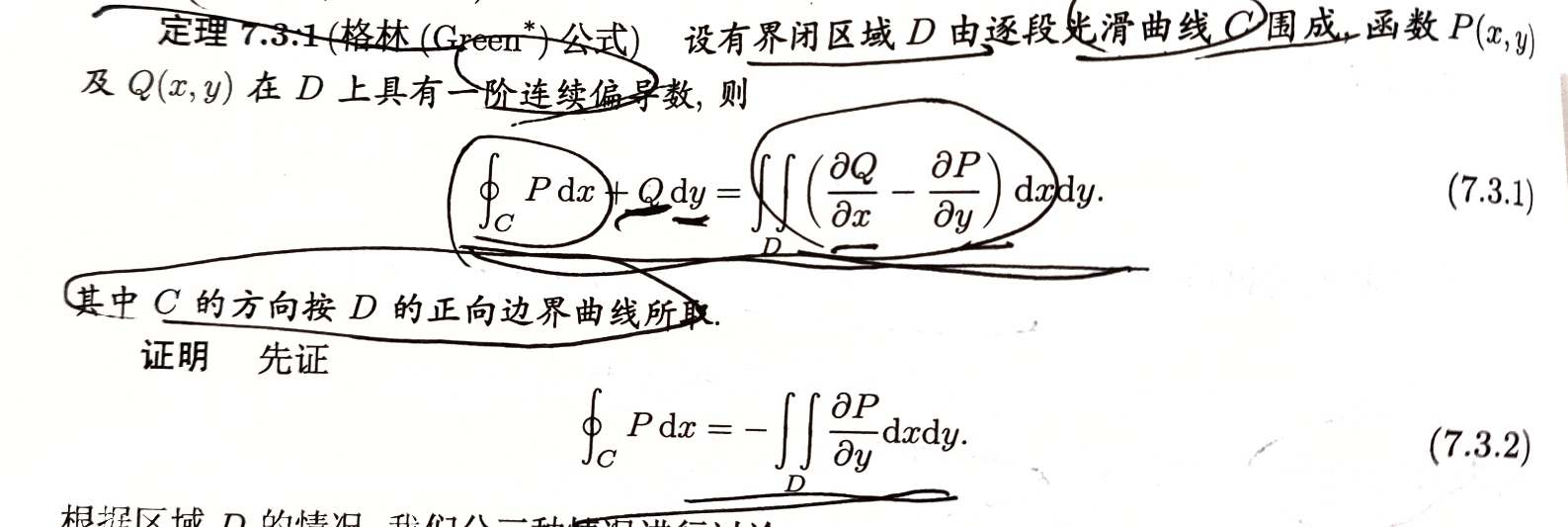
格林公式
格林公式的条件要求是曲线C是封闭曲线,构成了有界闭区域D,对C积分时沿逆时针正向。
格林公式求面积的应用:
第二类曲线积分与路径无关的条件
例子:
曲面积分
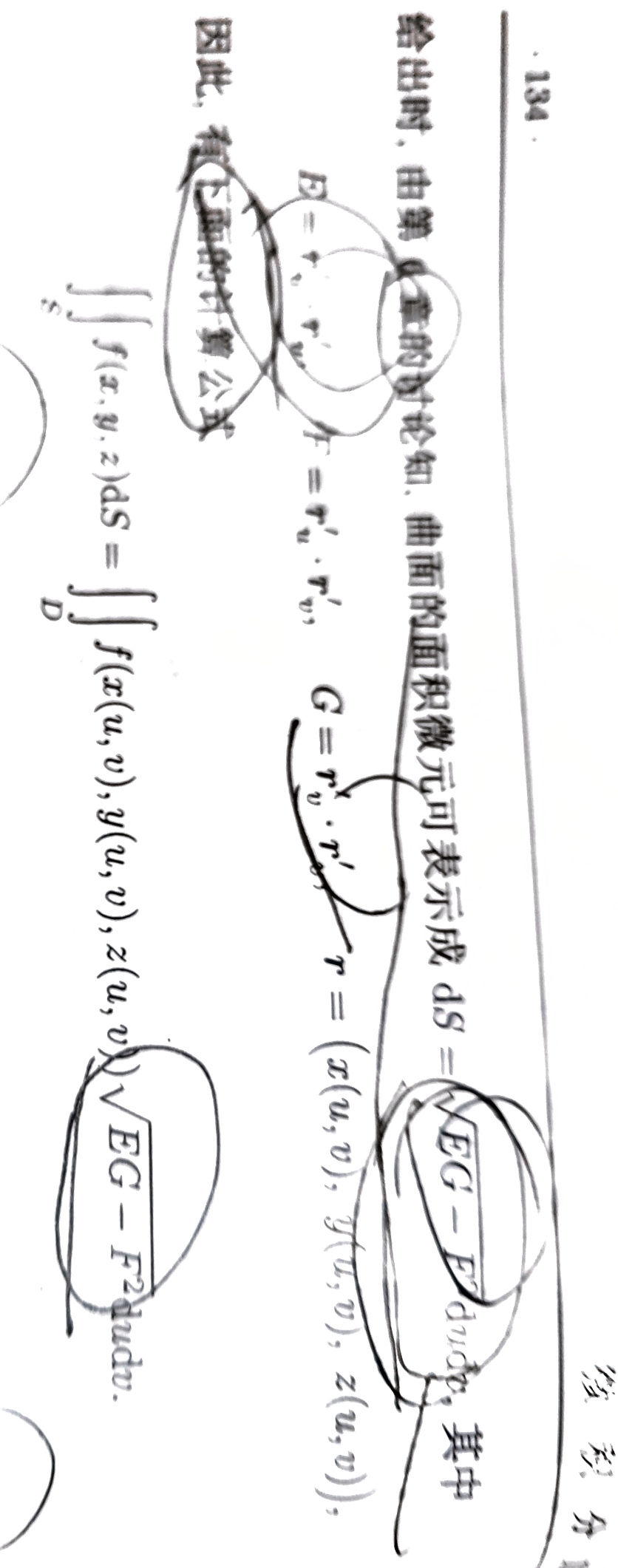
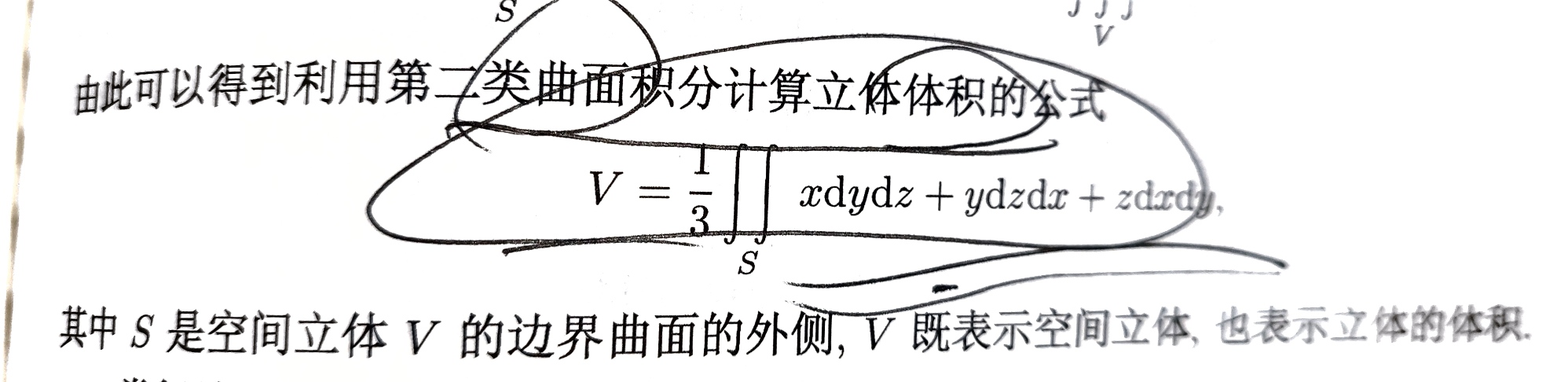
第一二类曲面积分
第二类曲面积分正负号条件:上正下负,右正左负,前正后负
高斯公式和斯托克斯公式
高斯公式
第二格林公式(利用高斯公式求解)
斯托克斯公式
无穷级数
常数项级数
柯西收敛原理:部分项的和对于任意给定的p,都能满足和小于$\epsilon$
正项级数
敛散性判别方法:
比较判别法(极限形式)
比值判别法
柯西判别法
柯西积分判别法
任意性级数
判断任意项级数收敛的方法:
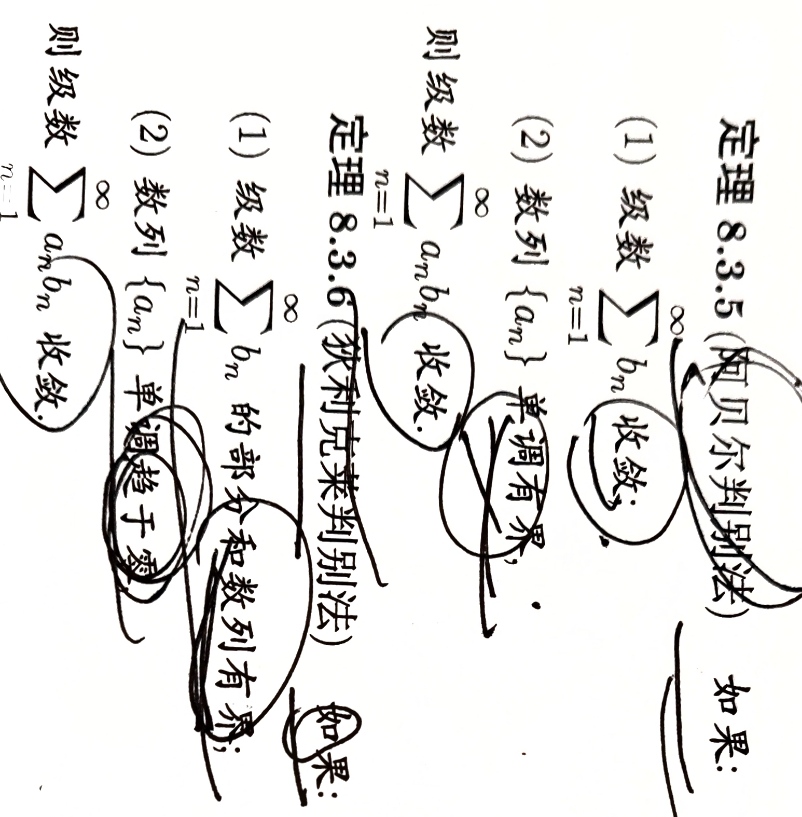
阿贝尔 1个收敛 1个单调有界
狄里克莱 1个部分和有界 1个单调趋于0
例题:
幂级数
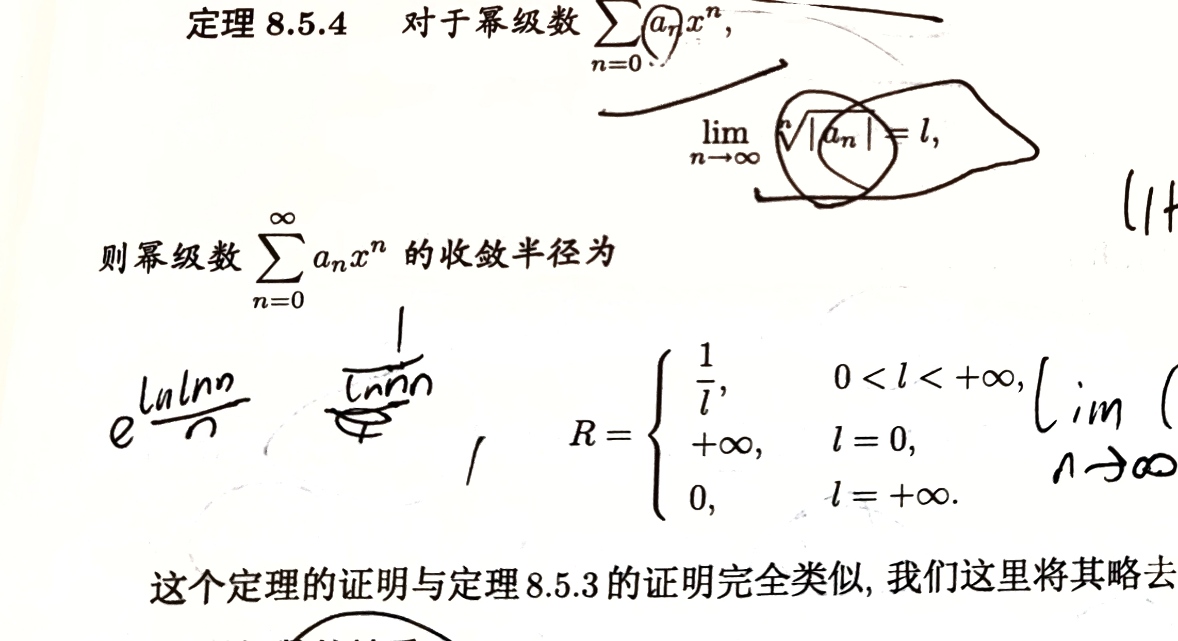
阿贝尔定理
斯特林公式
泰勒级数
广义积分敛散性
大部分与正项级数中的判别方法相似
柯西判别法:
傅里叶级数
任意周期是在积分内和积分外都乘上π/l
常微分方程初步
一阶微分方程的初等解法
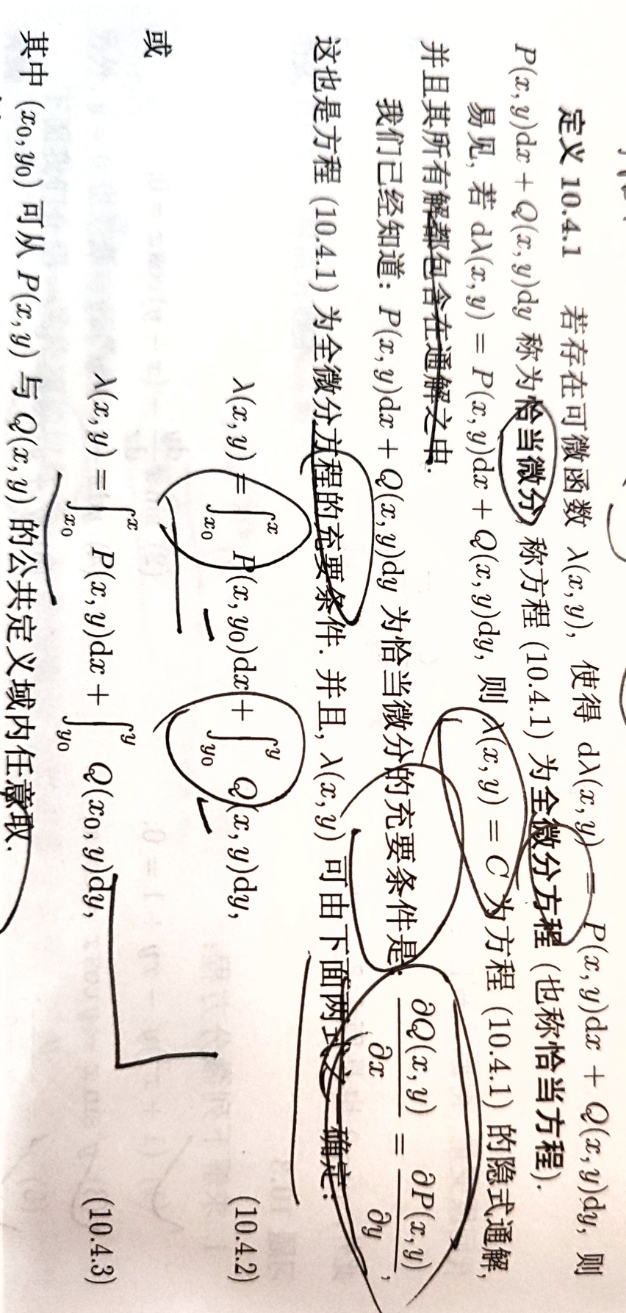
全微分方程
求积分因子的方法
高阶微分方程
可降阶的高阶微分方程:
设函数进行转换降阶
二阶线性微分方程:
二阶齐次线性微分方程
二阶非齐次线性微分方程
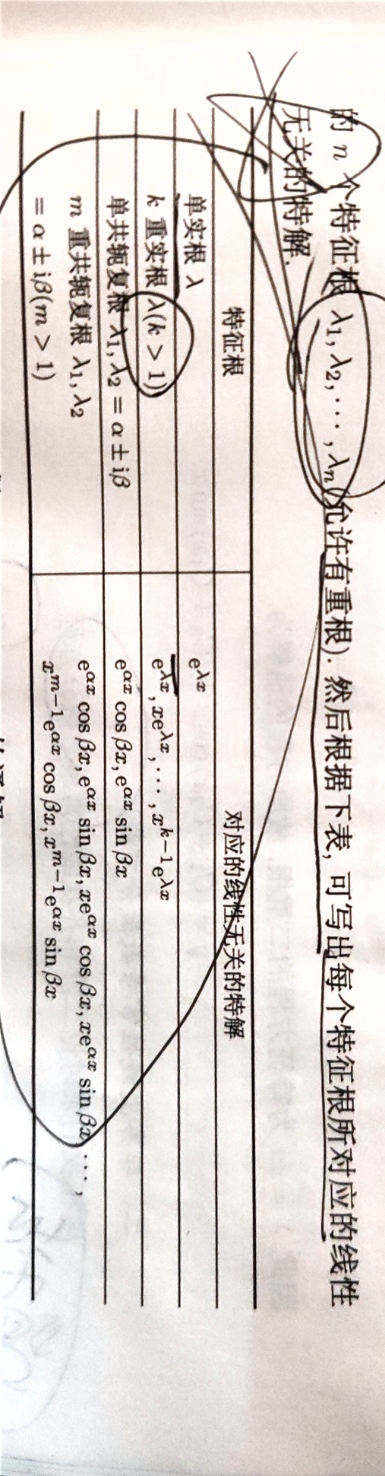
二阶常系数微分方程






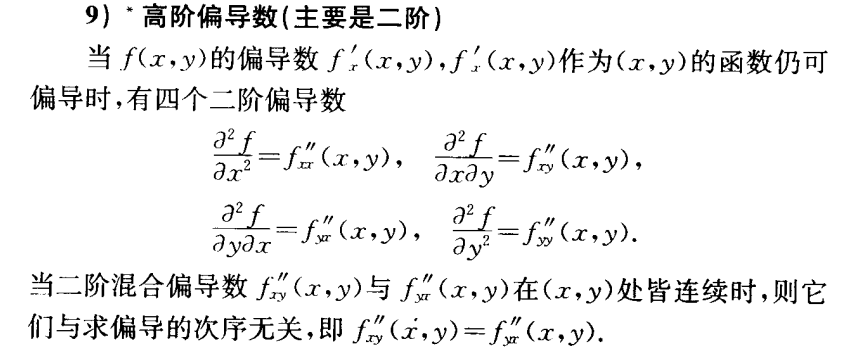
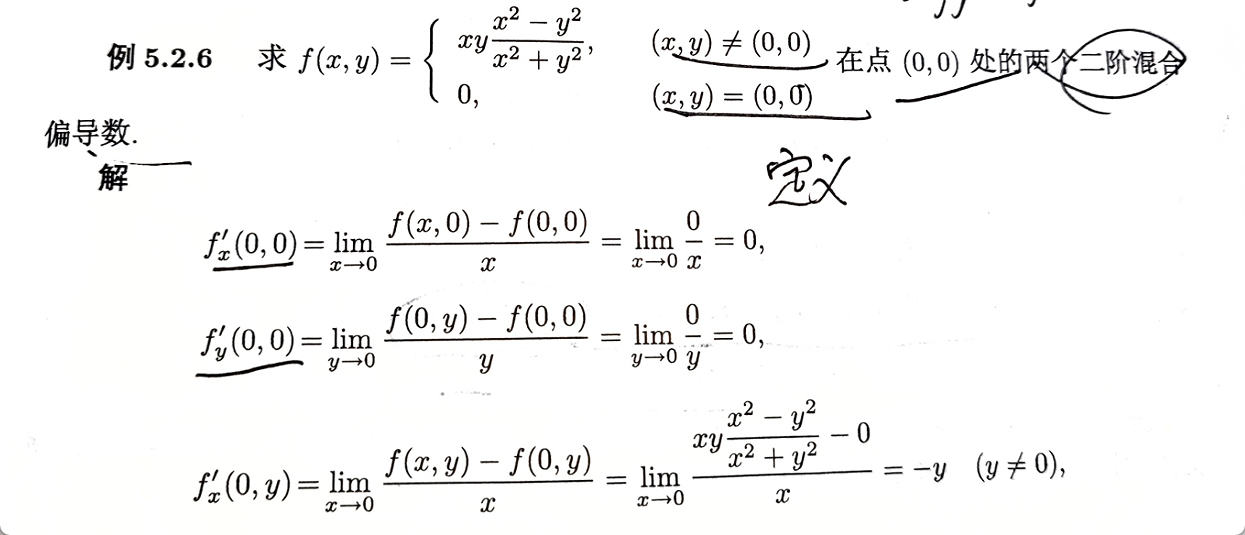
![RECTIFY_IMG_20240420_132347[1]](https://img.czruby.eu.org/imgs/2024-04-20-%E5%BE%AE%E7%A7%AF%E5%88%86%E4%BA%8C%E5%A4%8D%E4%B9%A0/RECTIFY_IMG_20240420_132347%5B1%5D.jpg)