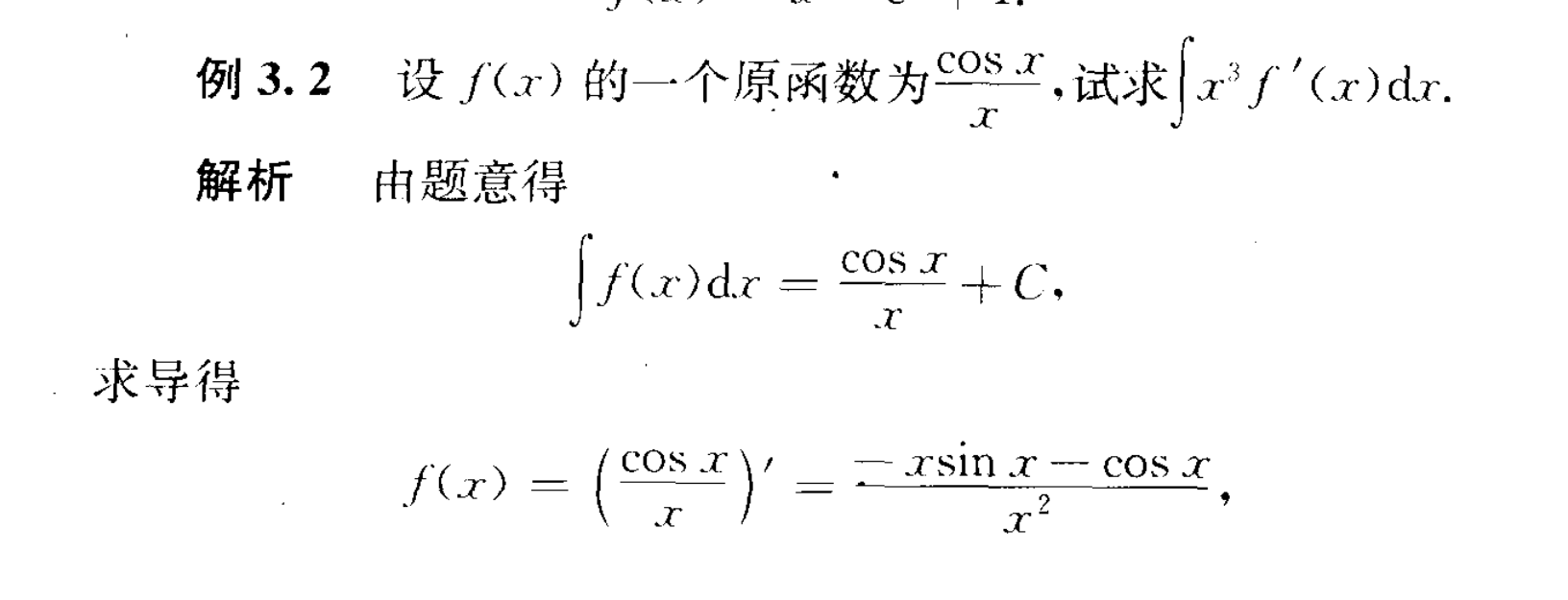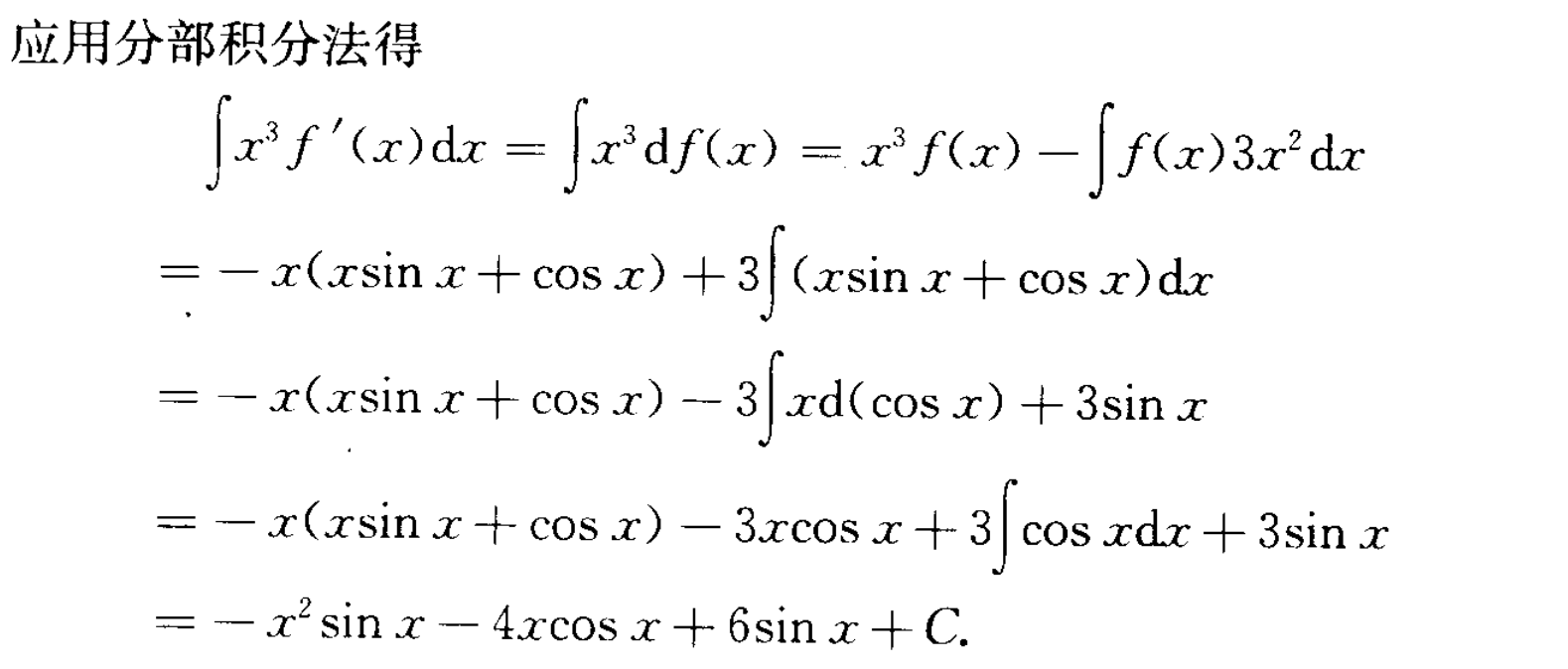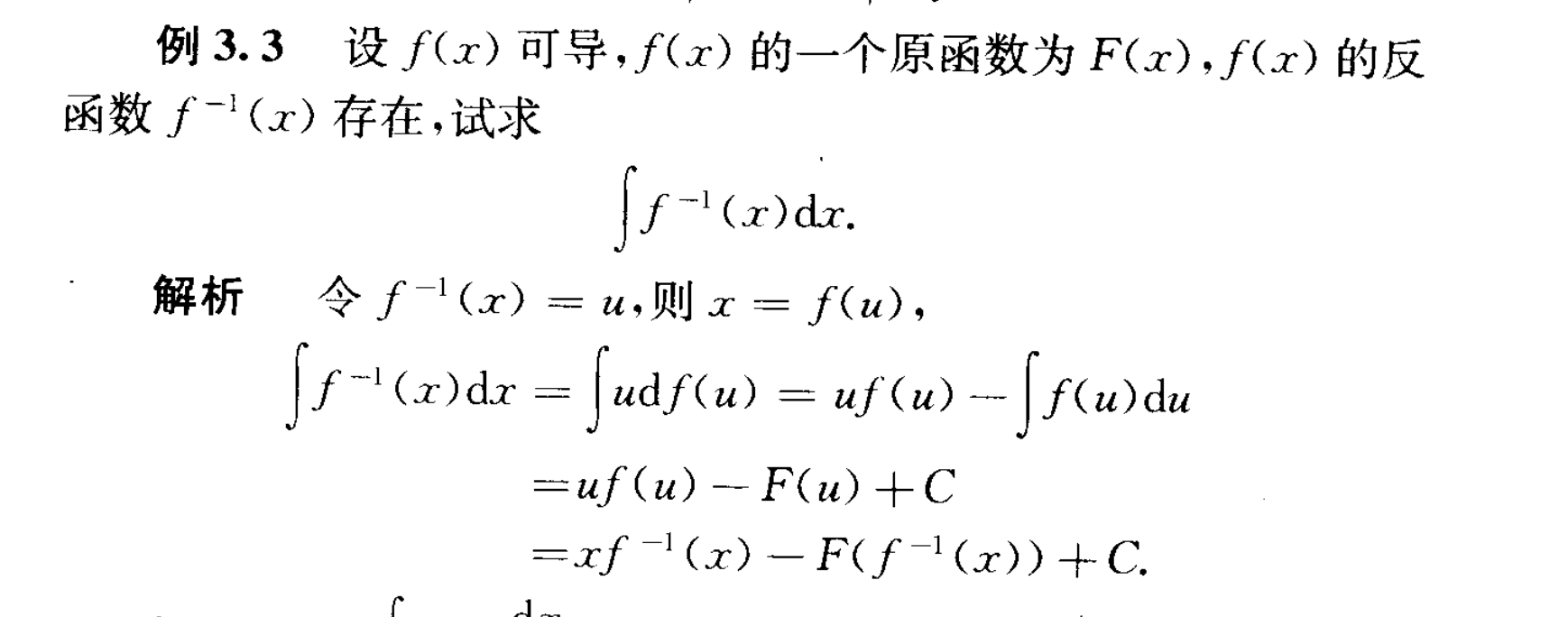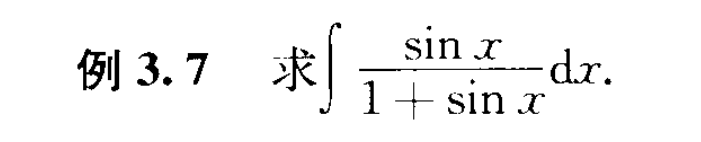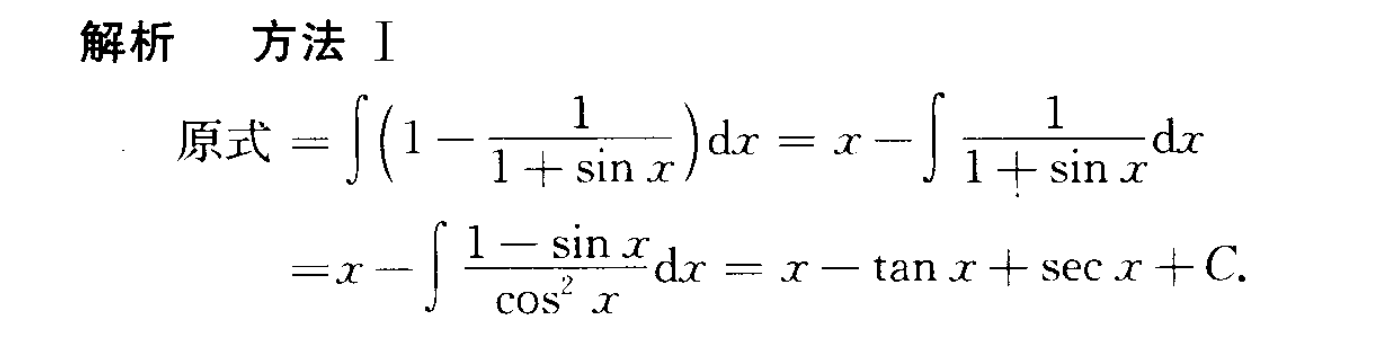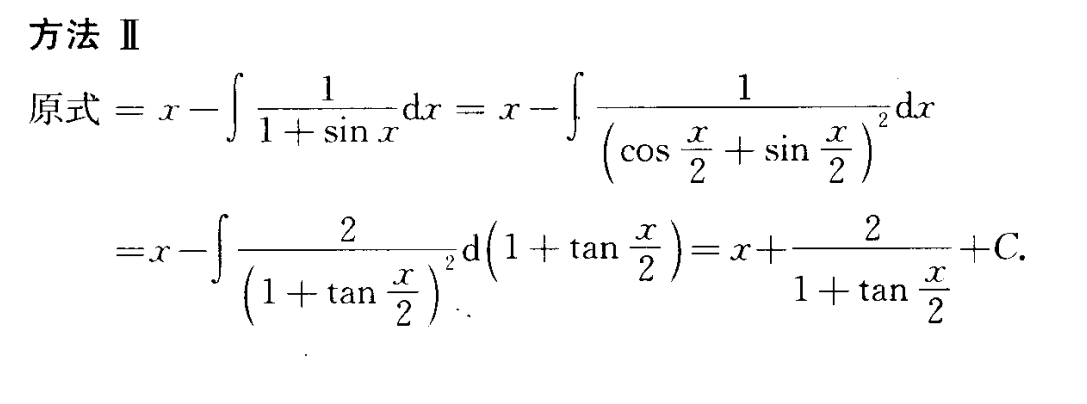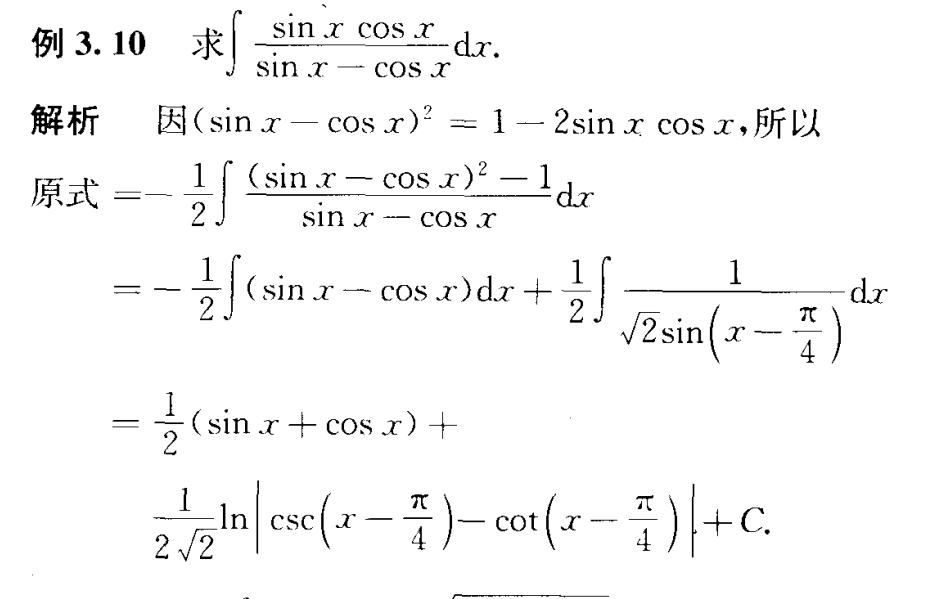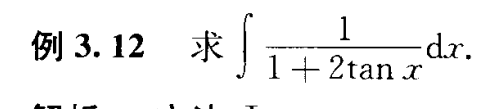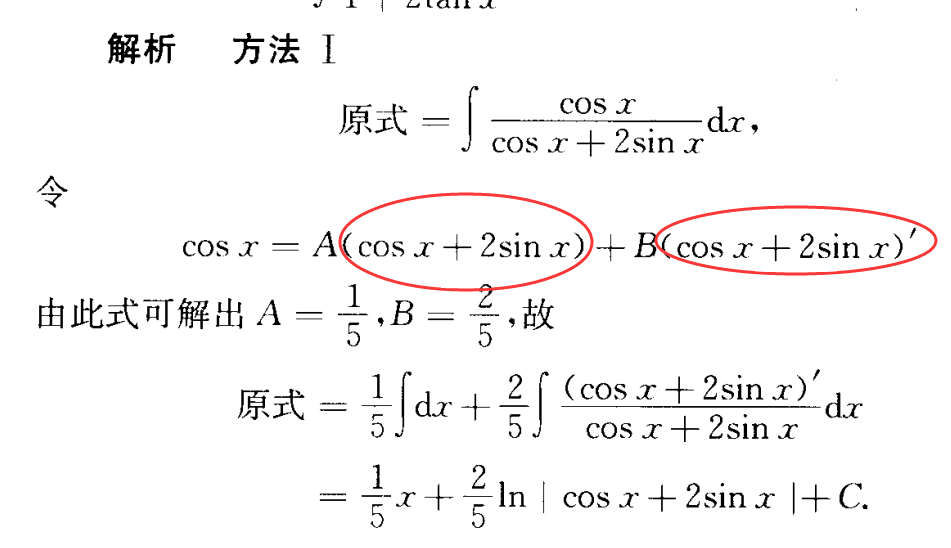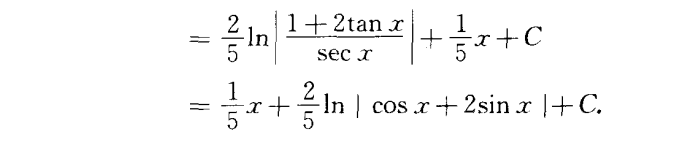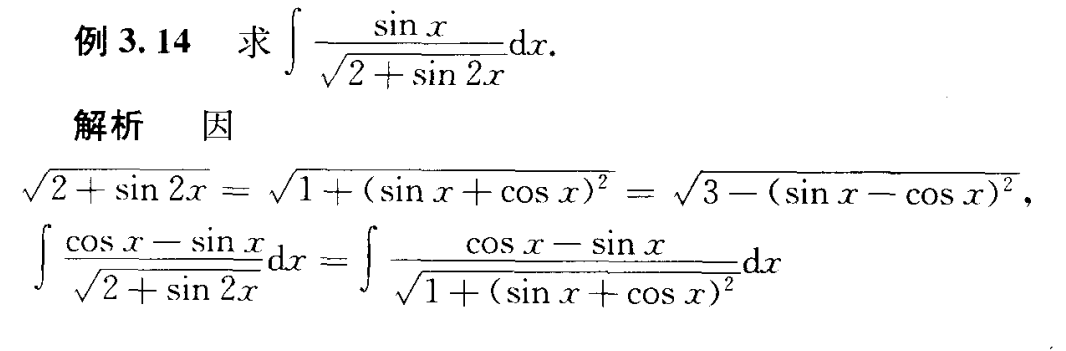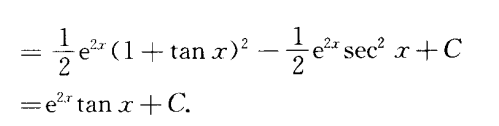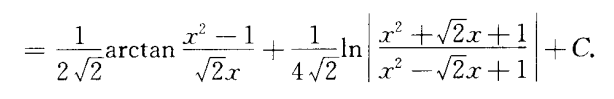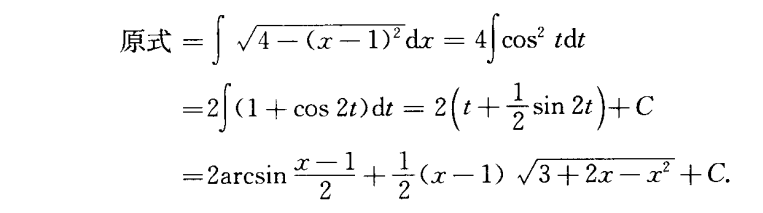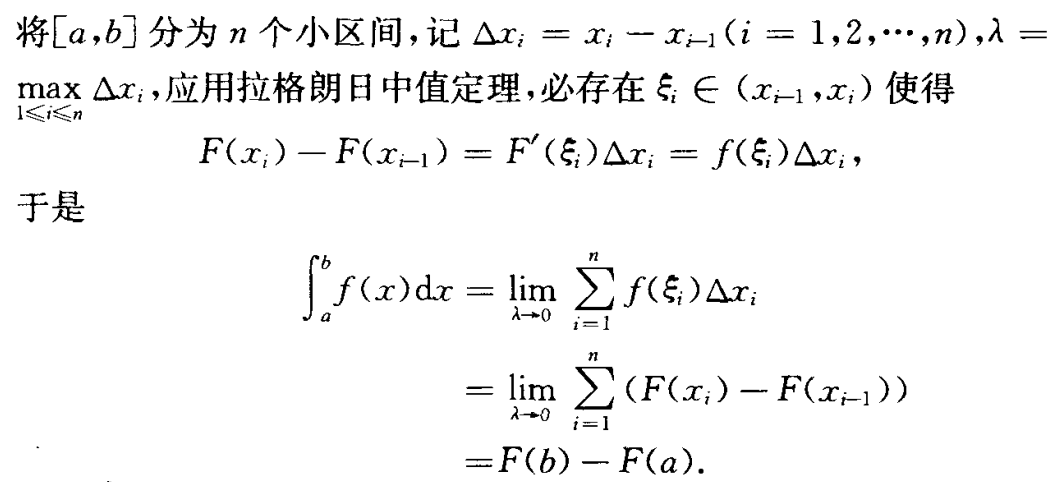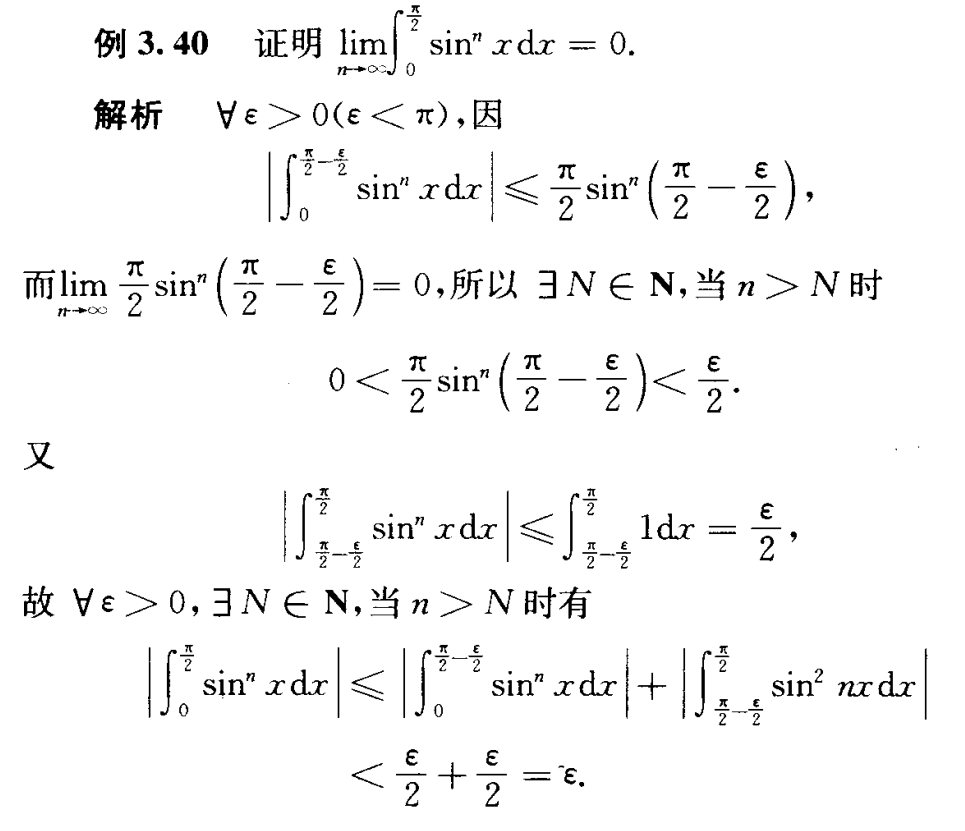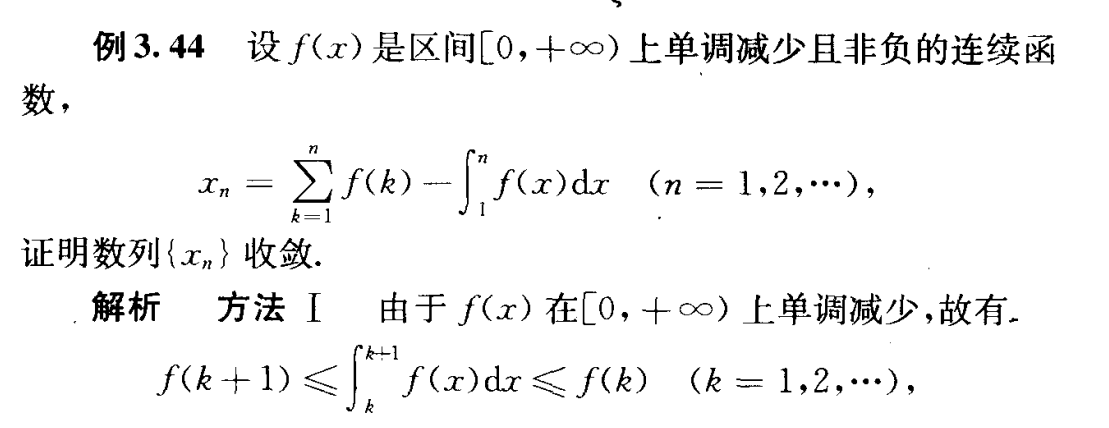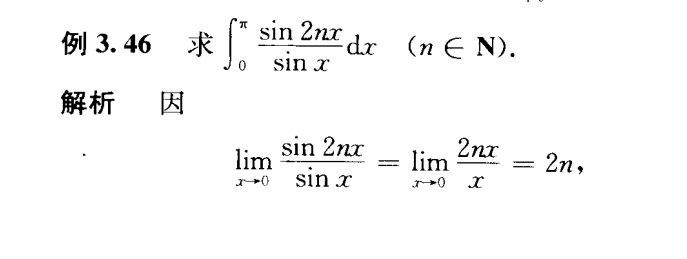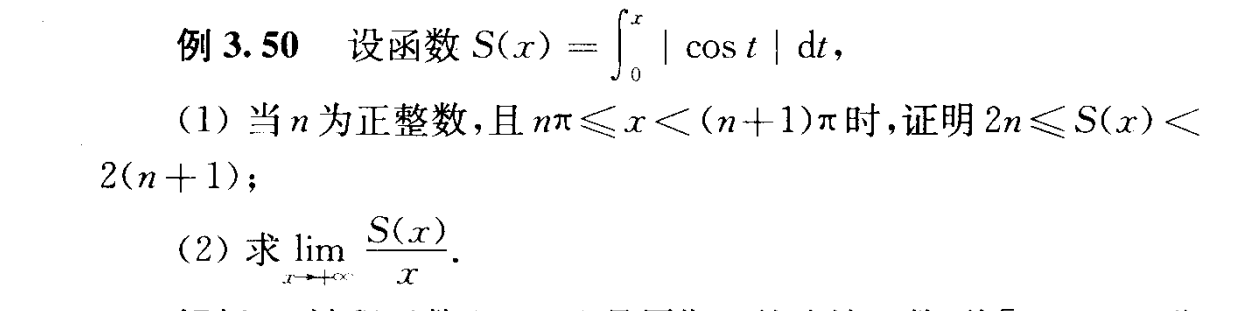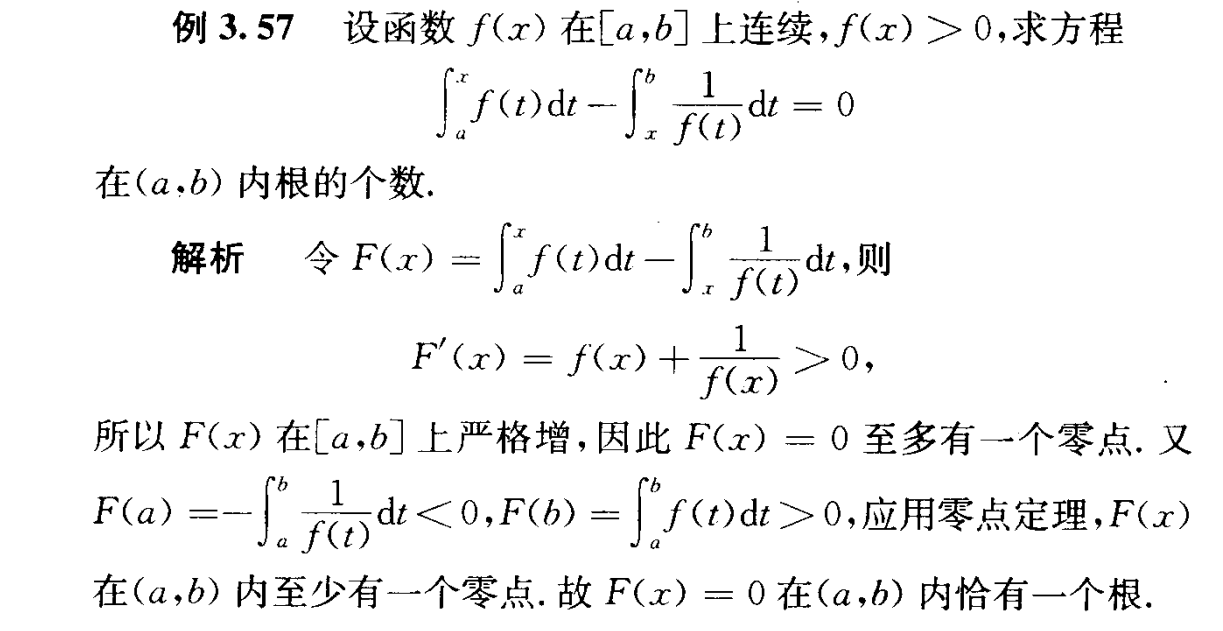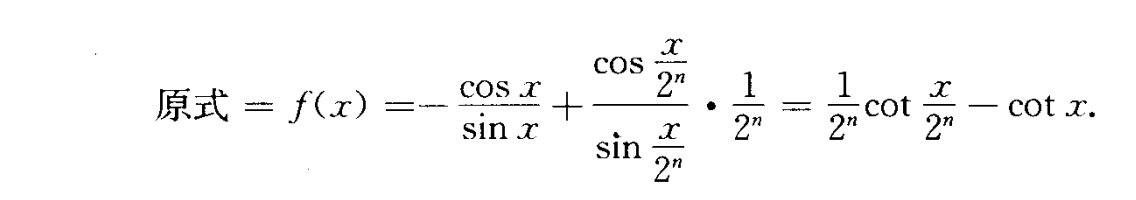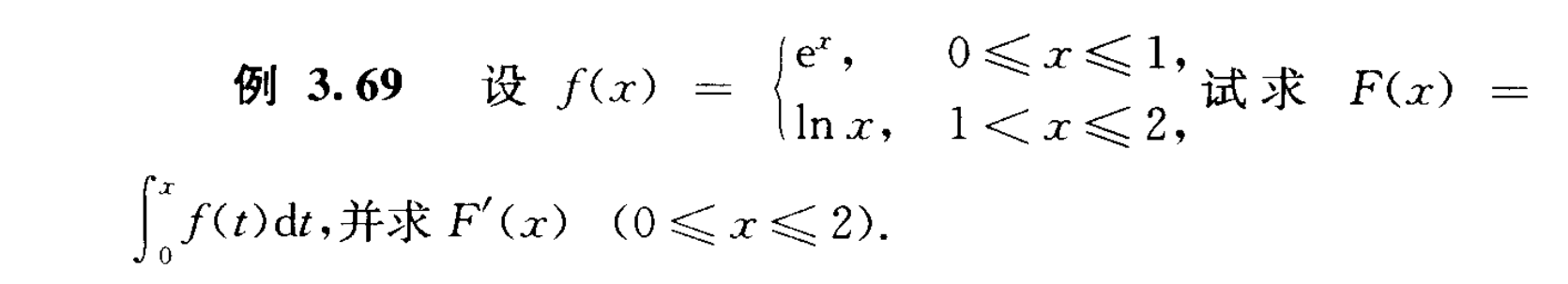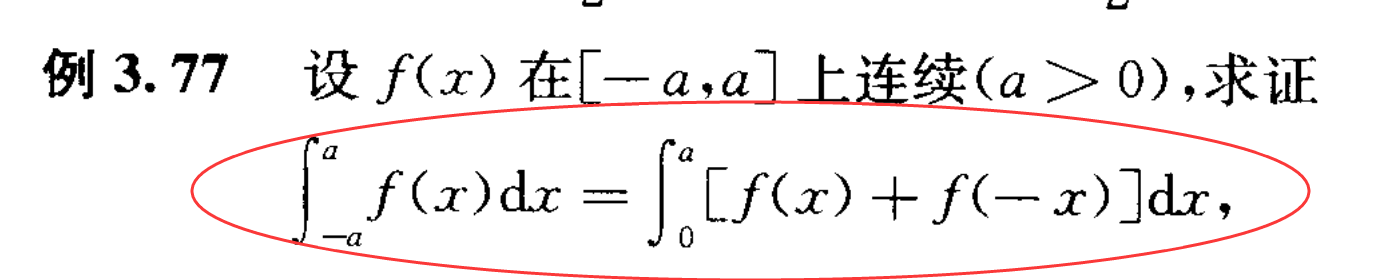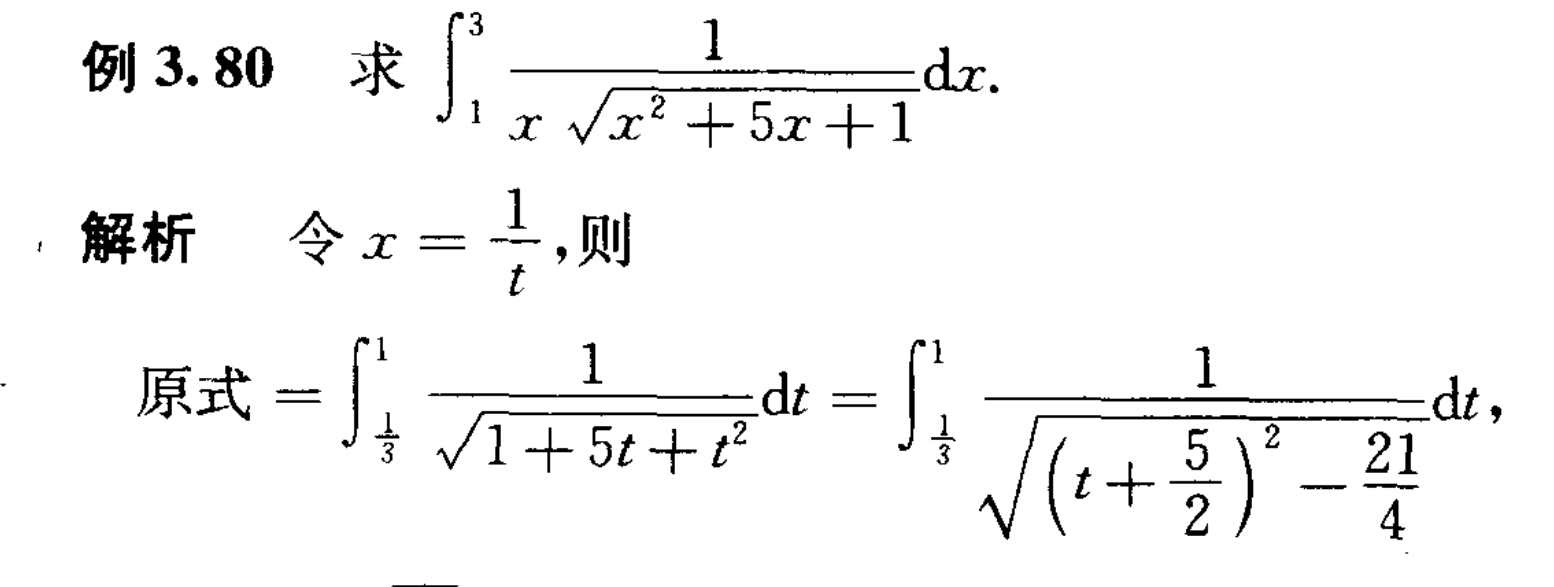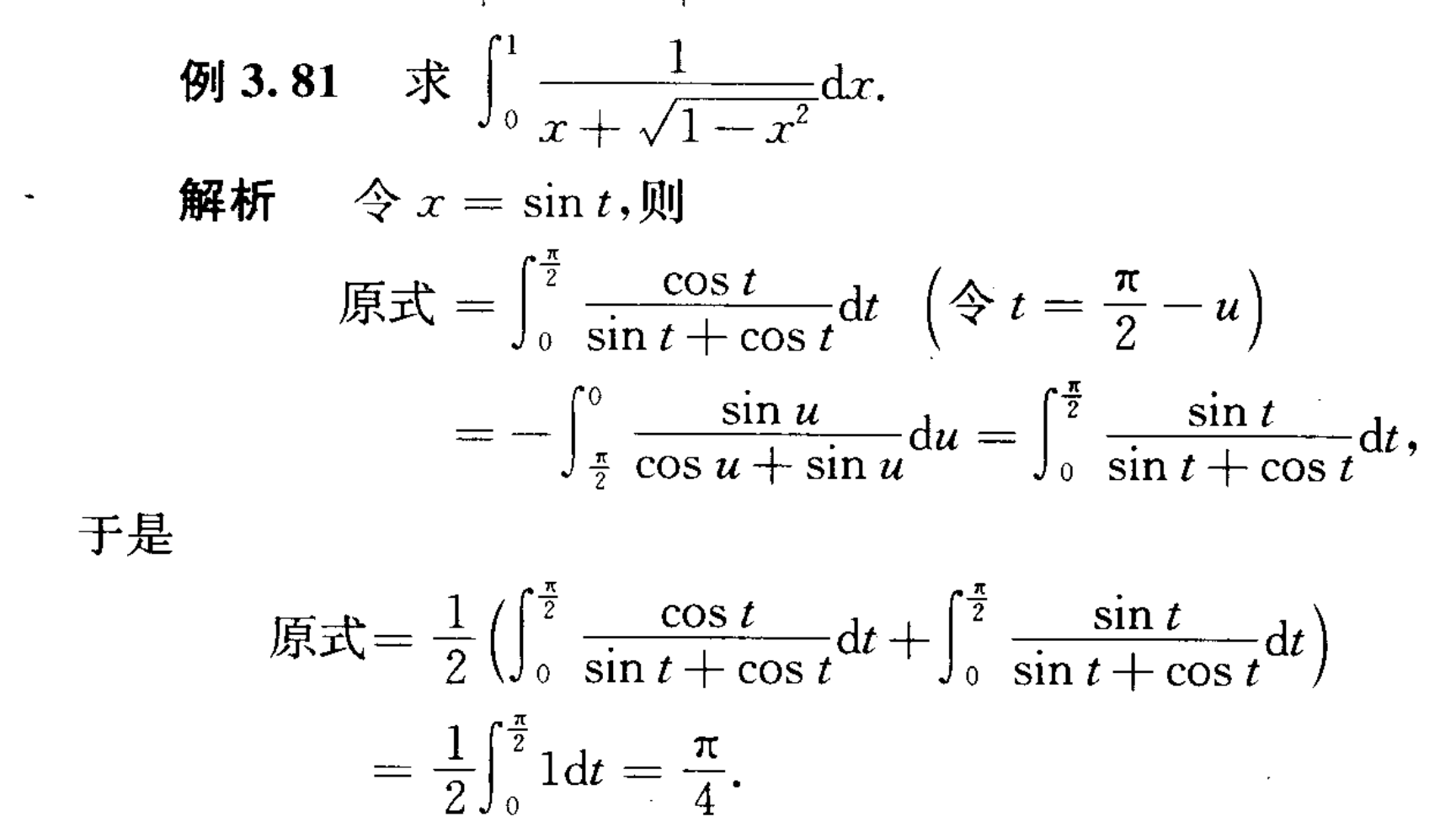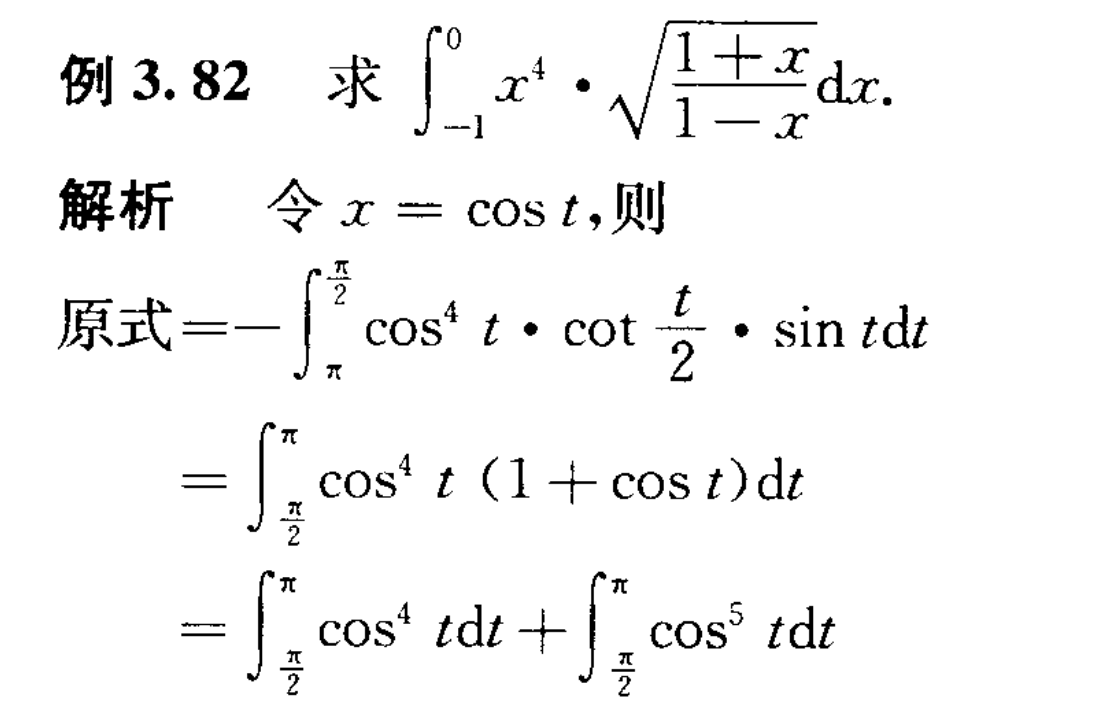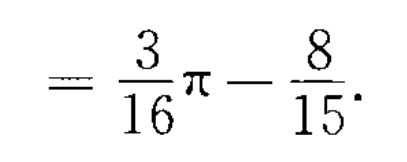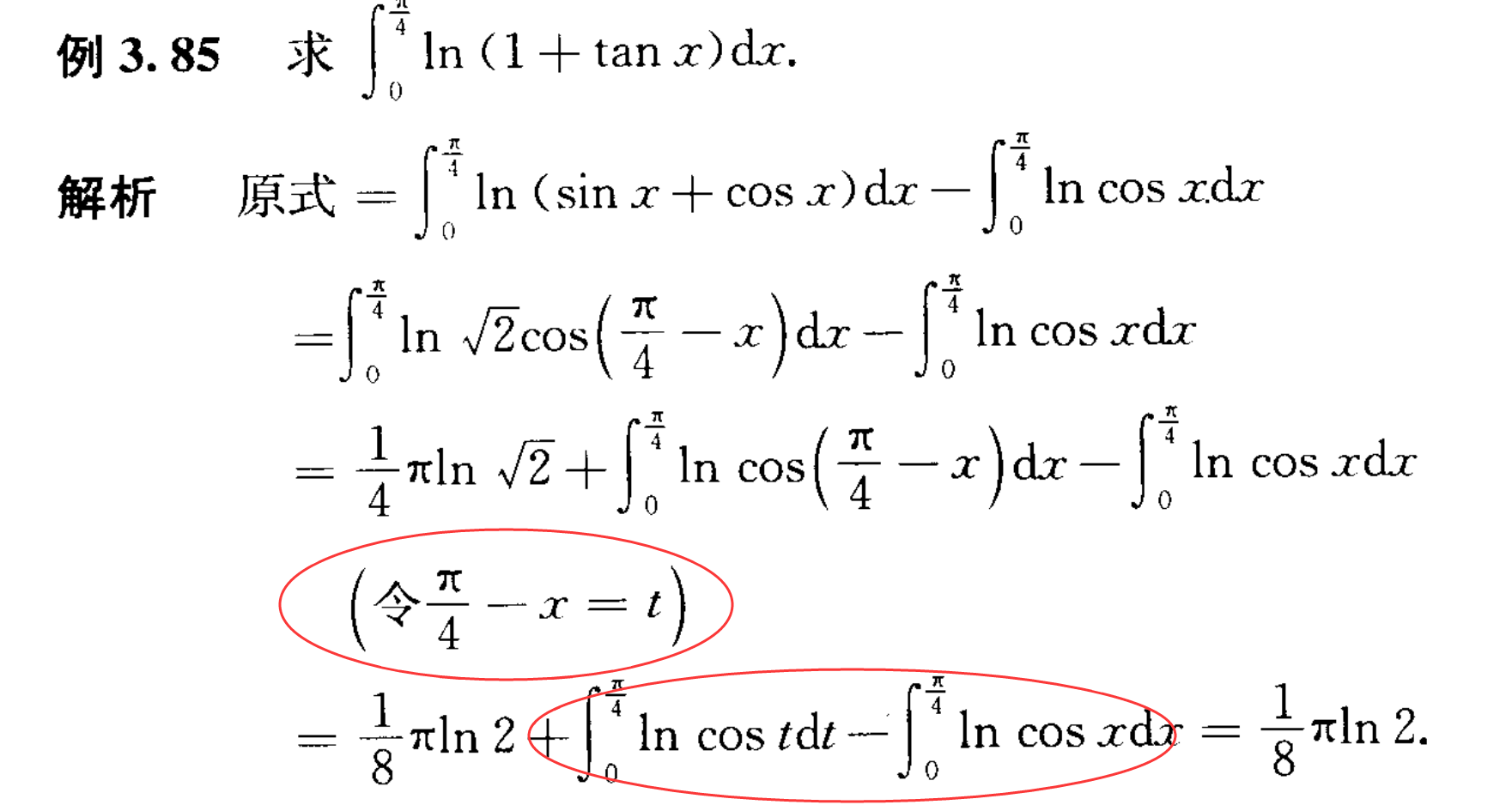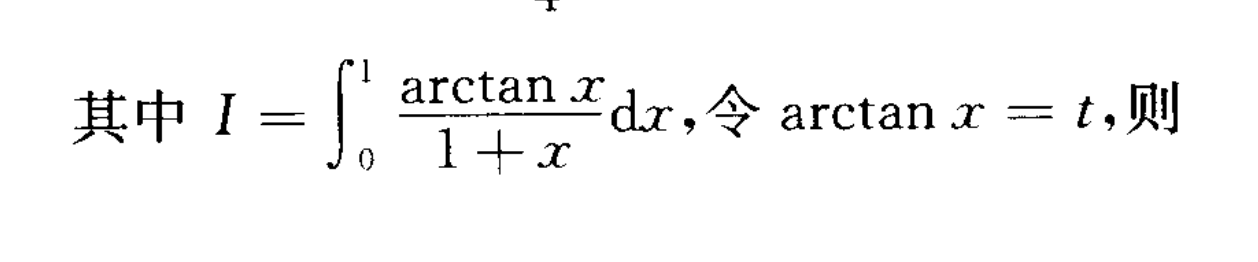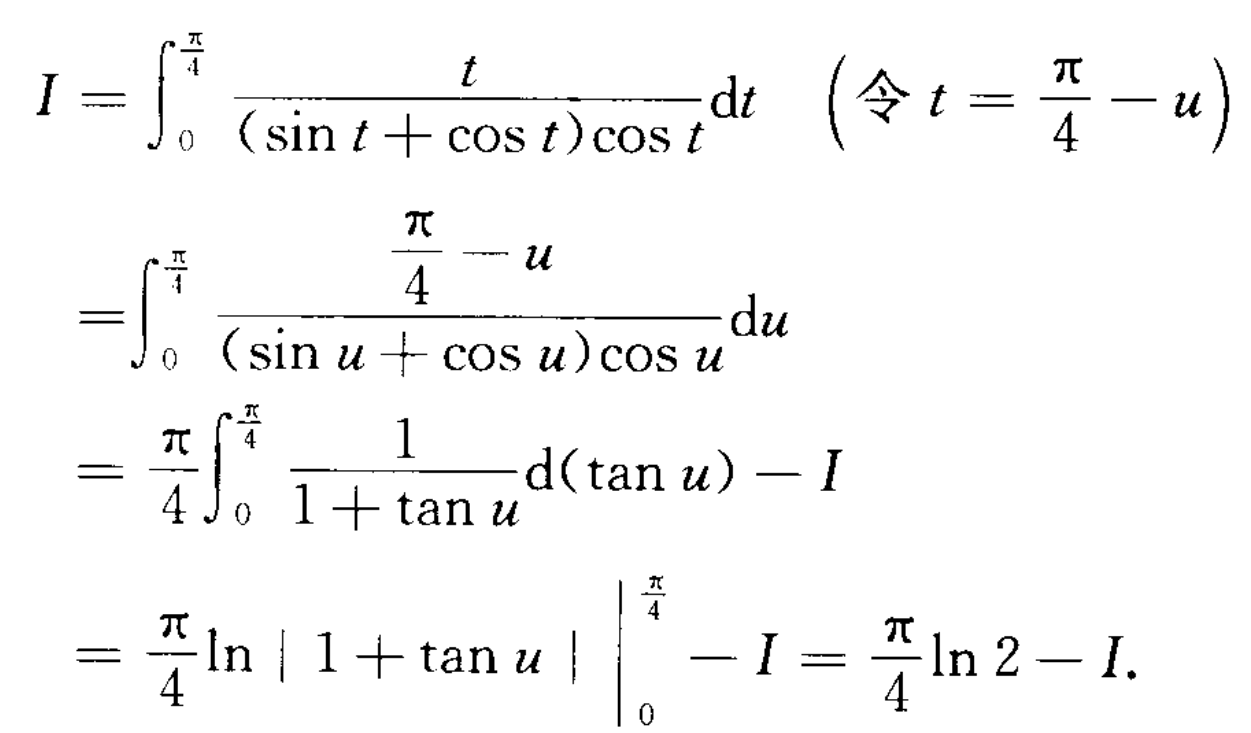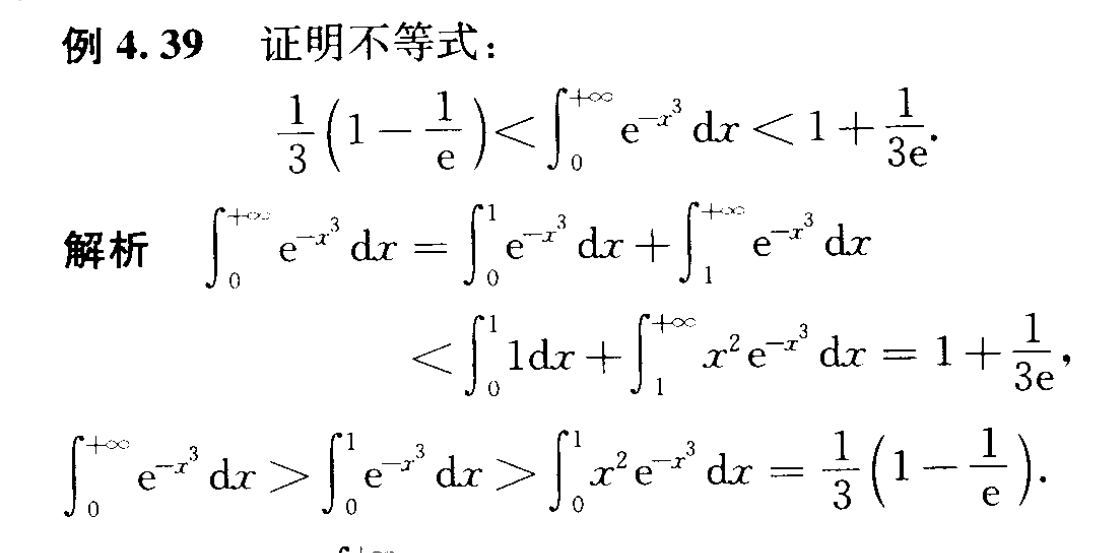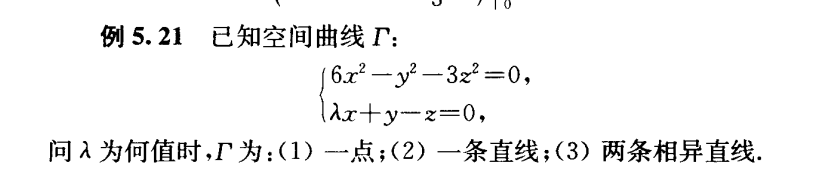不定积分与定积分
定积分使用分部积分
反函数
三角函数的多方法题
方法一: 巧妙使用三角函数配凑 $\int\frac{sinx}{cos^2x}dx=secx$
方法二: 三角换元
方法三:二倍角换元
三角函数整体代换
三角函数待定系数法
方法一:直接格式化待定系数
方法二:三角换元有理式化
这次不整体法了,分开积分
借助三角函数的变换,配凑得到结果
开局就拆开,升级全靠分部积分:star_struck:
$\int e^{2x}tanxdx$无法直接求出,非常奇妙的一题
难看出
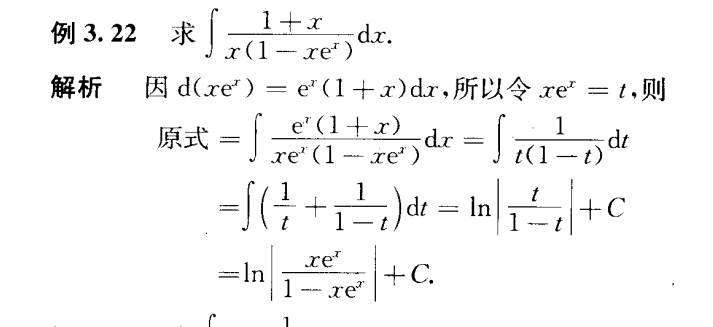 |
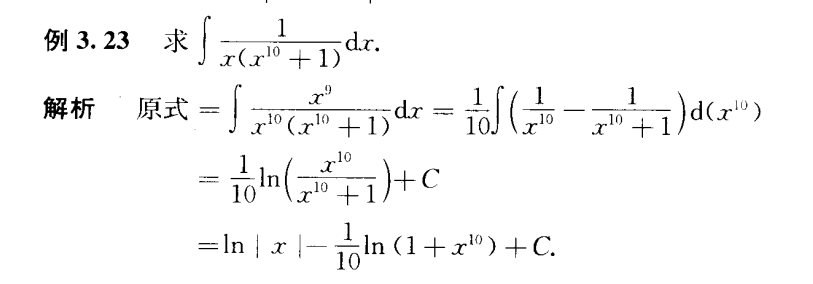 |
|---|
没见过,录了
你怎么这么会拆 :angry:
无理函数积分的例子$\sqrt{\frac{ax+b}{cx+d}}=t$
巧妙通分
无理函数积分的另一个例子
期末考试不会要出证明题吧
综合应用向来是不容易的
积分和极限,有意思
又是一道很新奇的证明题
这种类型题不难,也收集一道
积分中值定理和微分中值定理双应用
积分中值定理和数列收敛的结合
先判断是否是广义积分
很好一道题,第二问求导是我没有想到的
可以看一下可变积分的求导法则:
变限积分函数的求导
刚学会怎么求导,这题求导你就错了!
因为使用洛必达求导是无极限的,不代表原函数无极限,要换用别的方法求解极限。
结论是A哈
这题可以用求导了哈
求导结合零点定理
巧用积分再求导求函数值
这证明方法挺抽象的
看似人畜无害,但有扣分点
一个好像有用的公式
上面公式的简单应用
换元有时能把式子减少一项!
还有这种奇妙的求积分方式
不会换 :angry:
$cos^nx$和$sin^nx$的积分求法
一个换元一个不换!
巧妙换元相等求积分
又消掉了!
定积分的应用与广义积分
一道很好的证明题
求交点麻烦,使用整体代换的思想
对于无法直接求体积的几何体,可以通过切割,使切割的平面的面积以F(x)的形式变化,再通过$\int f(x)dx$进行计算
分部积分可能会出现两项发散的项,而先求原函数再牛莱公式可以消掉发散项从而求出积分
广义积分转为简单定积分,换元很关键
这种放缩是很难想到的
参数讨论收敛性
空间解析几何
参数方程解出交点
其中方法一:设方向向量,利用几何关系解出方向向量
方法二:设出所求直线所在平面的方程,利用相交条件求出交点,用交点和恒过定点求出方向向量
方法三:利用另一条直线的平面束和恒过定点确定另一个平面,用平面相交一般式确定直线方程
求两直线公垂线方程的方法,仍利用参数方程求交点
求旋转曲面方法
含参数的空间曲线,求参数范围产生不同的曲线
主要方法是确定一个变量的值,然后将方程组转化为两变量的方程,使用韦达定理得出结果
评论