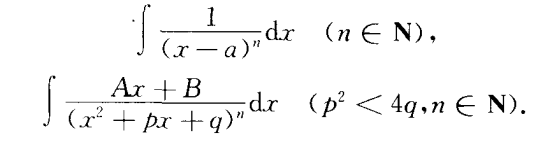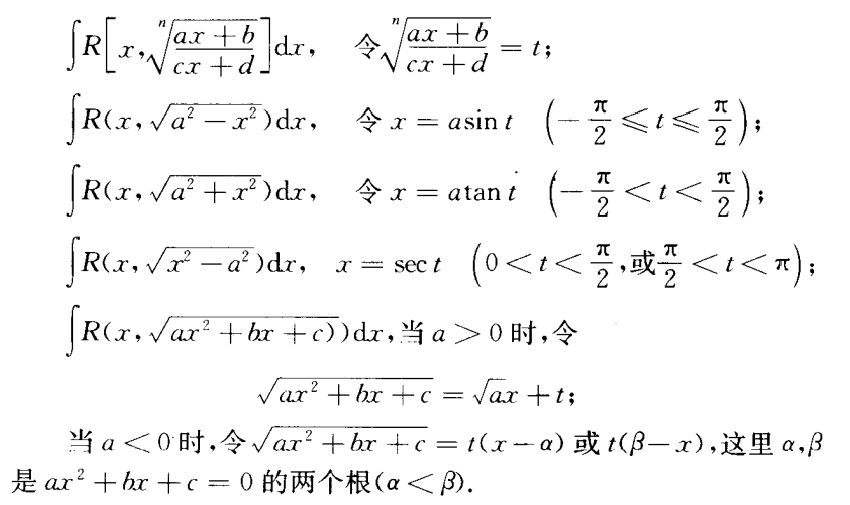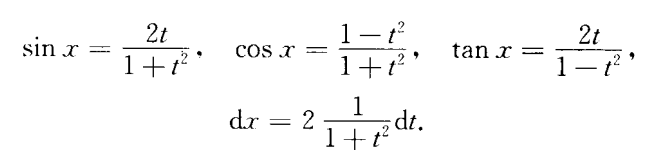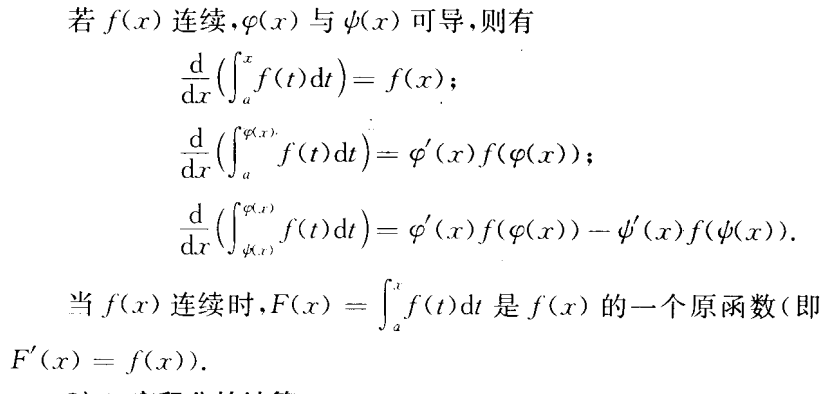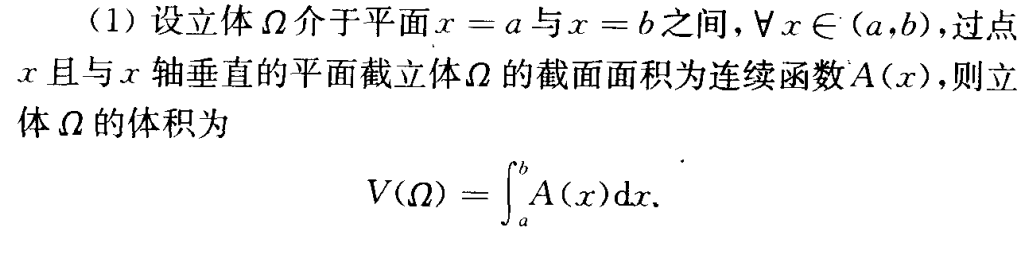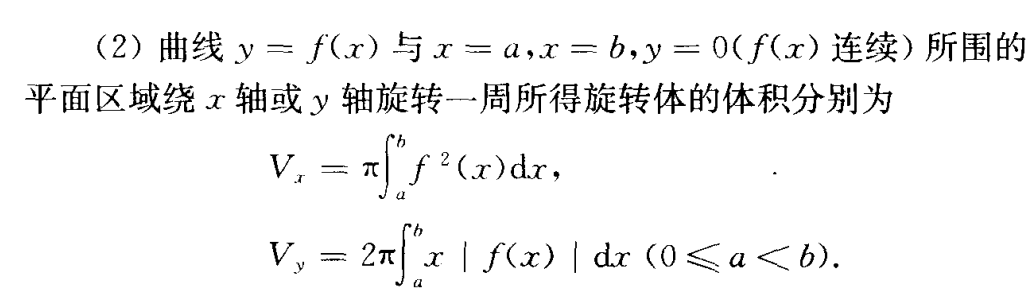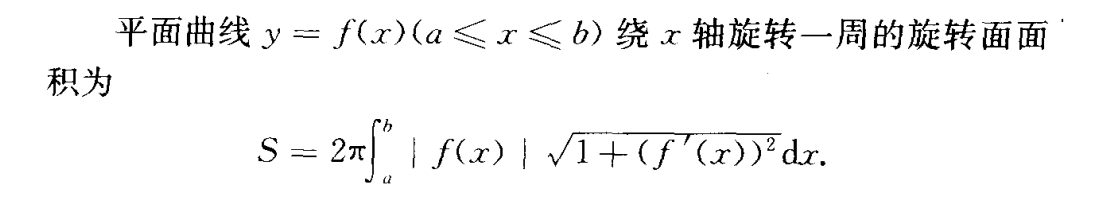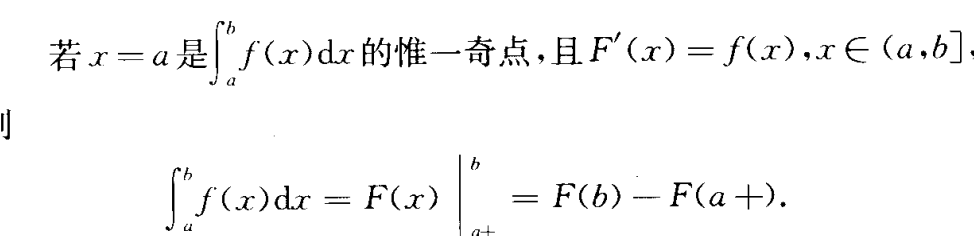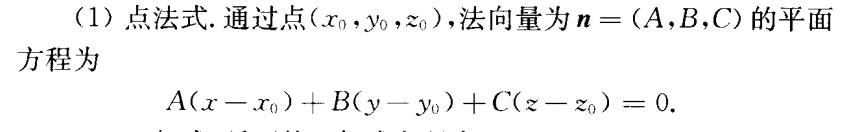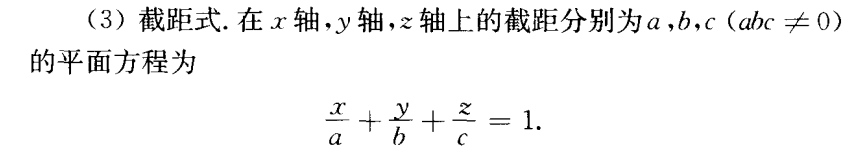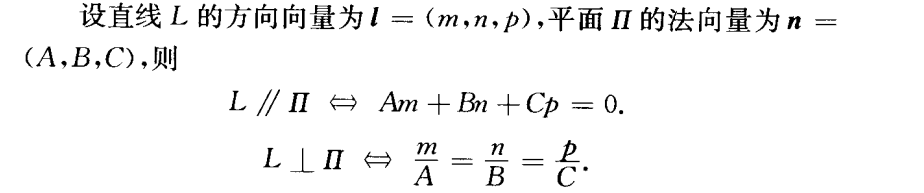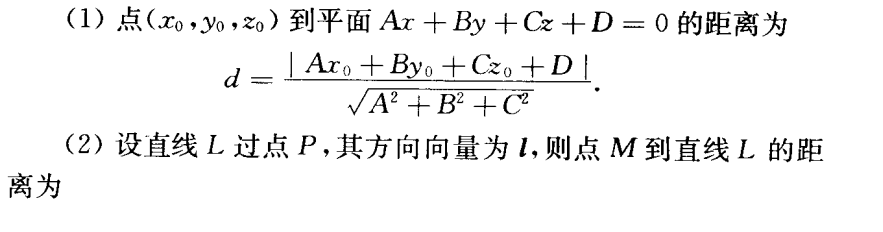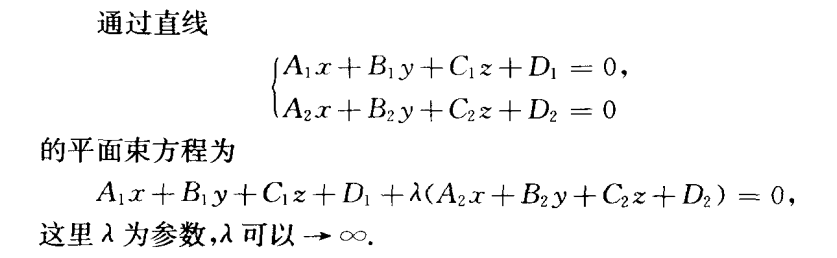微积分期末复习

第三章：不定积分与定积分

不定积分

常见不定积分公式：

积分方法：

• 换元积分

• 分部积分
  分部积分法之列表积分法

• 有理函数的积分

  任一有理函数可分解为一多项式和若干分式的和

  
  
  

  轻松快速解决有理函数积分的拆解

• 简单无理函数积分

  

• 三角函数有理式的积分

  当$tan\frac{x}{2}=t$时

  

定积分

定积分的主要性质

1. 保向性

   若$f(x),g(x)$可积，$f(x)\leq g(x),\forall x\in[a,b],f(x)\neq g(x)$
   $$ \int_{a}^{b}f(x)dx\leq\int_a^bg(x)dx$$

2. 可加性
   $$ \int_{a}^{b}f(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx$$

3. 积分中值定理
   若$f(x),g(x)$皆在$[a,b]$上连续，$g(x)$定号（均大于等于0，或均小于等于0）,则存在 $\xi\in(a,b)$,使得
   $$ \int_{a}^{b}f(x)g(x)dx=f(\xi)\int_a^bg(x)dx$$

函数的平均值

$$\overline{y}=\frac{1}{b-a}\int_a^bf(x)dx $$

变限的积分

变限积分函数的求导

定积分计算

• 牛顿莱布尼茨公式
• 换元积分
• 分部积分
• 定积分性质（函数奇偶性、周期函数）

第四章：定积分的应用与广义积分

定积分的应用

平面图形的面积

特殊立体的体积

平面曲线的弧长

积分号右边部分即为对应弧微分

旋转面的面积（结合弧微分）

广义积分

两类广义积分的概念

两类广义积分的计算

1. 广义牛顿-莱布尼兹公式
   
   
2. 广义换元积分
3. 广义分部积分

Euler积分—B函数与Γ函数

了解即可

Euler积分—B函数与Γ函数

第五章：空间解析几何

空间直角坐标系的相关概念

向量的基本概念

向量运算性质

空间平面的方程

1. 点法式
   
2. 一般式
   
3. 截距式
   
4. 三点式
   

空间直线的方程

1. 点向式（标准式）

   方向向量（l,m,n）,过点(x0,y0,z0)

   $\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}$

2. 参数式

   $x=x_0+lt$ ……

3. 两点式

   $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

4. 一般式

   两平面方程联立

平面与平面的关系

直线与直线的关系

直线与平面的关系

这里和前面的平行垂直不一样

点到平面（直线）的距离与异面直线的距离

平面束

曲面方程

二次曲面的标准方程

空间曲线方程